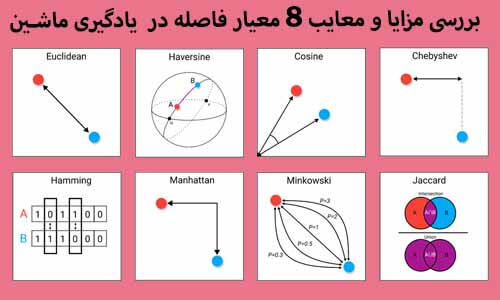
مزایا و معایب 8 معیار فاصله در داده کاوی و یادگیری ماشین

درک اینکه از کدام معیار فاصله در الگوریتمها استفاده کنیم بسیار مهم است . نوع معیار فاصله خیلی در عملکرد الگوریتمها تاثیر گذار است. برای مثال در الگوریتم knn به طور پیش فرض از معیار فاصله اقلیدسی استفاده می‌کنند. ولی سوال این است که اگر ابعاد داده بسیار بالا باشد باز هم معیار فاصله اقلیدسی میتواند یک معیار مناسبی باشد؟ یا اگر داده ی شما شامل اطلاعات مکانی باشد باز هم فاصله اقلیدسی میتواند معیار مناسبی باشد؟ شاید فاصله haversine معیار مناسبی برای چنین داده‌ای باشد!

دانستن اینکه از چه فاصله ای استفاده کنیم، به ما کمک میکند یک الگوریتم ضعیف رو به یک الگوریتم بسیار دقیق تبدیل کنیم.

نکته: برای برخی معیارهای فاصله لازم است که یک پست جدایی بنویسیم و به طور مفصل در مورد مزایا و معایب آنها صحبت کنیم. در این بخش سعی میکنیم به طور مختصر مزایا و معایب معیارهای فاصله رو بررسی کنیم.

فاصله اقلیدسی (Euclidean Distance)

با رایجترین معیار فاصله، یعنی فاصله اقلیدسی شروع می کنیم. معیاری است که میتوان آنرا با محاسبه طول دو نقطه متصل بهم توصیف کرد. معیاری که به بهترین وجه می‌تواند به عنوان طول یک قطعه متصل به دو نقطه توضیح داده شود. فرمول فاصله اقلیدسی بسیار ساده است و برای محاسبه فاصله دو نقطه در مختصات دکارتی از قضیه فیثاغورث استفاده می‌کند. فاصله اقلیدسی کوتاه ترین مسیر بین دو نقطه را به عنوان فاصله پیدا می‌کند.

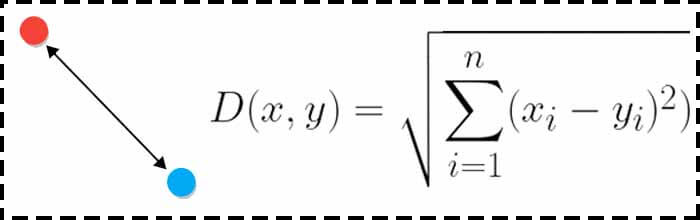
معایب فاصله اقلیدسی (Euclidean Distance)

با اینکه فاصله اقلیدسی یک معیار رایجی در بین الگوریتم‌ها است ولی باید بدانیم که این معیار به مقیاس داده وابسته است.  به عبارتی scale invariant  نیست و اگر مقدار ویژگی‌ها متفاوت باشد فاصله بدست آماده تغییر می‌کند. اگر بخواهیم از این معیار استفاده کنیم بهتر است در ابتدا مقدار ویژگی ها را نرمال کنیم. علاوه‎‌براین ، هر چقدر ابعاد داده افرایش یابد به همان میزان این معیار ناکارامدتر میشود.

 چه زمانی از فاصله اقلیدسی استفاده کنیم؟

فاصله اقلیدسی در ابعاد پایین خیلی خوب عمل می‌کند. الگوریتمی مثل knn نشان داده است که اگر ابعاد داده پایین باشد، فاصله اقلیدسی بسیار خوب عمل می‌کند. با اینکه معیارهای زیادی در جهت بهبود ایرادات فاصله اقلیدسی مطرح شده اند ولی همچنان از فاصله اقلیدسی بسیار استفاده می‌شود. دلیلش هم سادگی پیاده‌سازی و عملکرد عالی در بسیاری از موارد است.

معیار تشابه کسینوسی (Cosine distance)

از معیار شباهت کسینوسی به عنوان یک راه برای حل مشکل فاصله اقلیدسی در ابعاد بالا استفاده می‌کنند. فاصله بین دو نقطه در معیار شباهت کسینوسی به طور ساده کسینوس زاویه بین دو نقطه (بردار) است. این فاصله رو میتوان با ضرب نقطه‌ای بین دو بردار بدست آورد، به شرط اینکه هر دوبردار نرمال شوند.

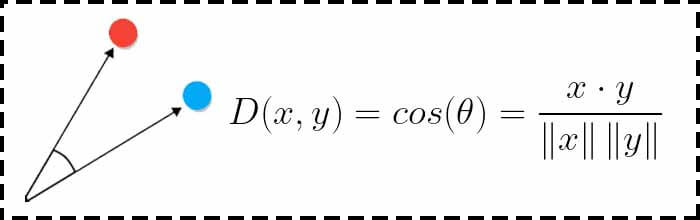
اگر دو بردار دقیقا در یک جهت (راستا) باشند در این صورت شباهت کسیونسی آنها برابر یک خواهد بود.  و اگر جهت دو بردار کاملا متضاد هم باشد در این صورت شباهت کسینوسی آنها برابر منفی یک خواهد بود. به این نکته توجه کنیم که دامنه بردار‌ها اهمیتی در این معیار فاصله ندارد و فقط جهت بردارها اهمیت دارد.

معایب تشابه کسینوسی (cosine similarity)

یکی از معایب تشابه کسینوسی این است که دامنه بردارها اهیمت ندارند و در پروسه محاسبه فاصله مورد استفاده قرار نمی‌گیرند. در عمل، این بدان معنی است که تفاوت در مقادیرها به طور کامل در نظر گرفته نمی‌شود. به عنوان مثال اگر سیستم پیشنهاد دهنده را در نظر بگیرید، در تشابه کسینوس اختلاف مقیاس رتبه‌بندی بین کاربران مختلف در نظر گرفته نمی‌شود.

 چه زمانی از تشابه کسینوسی استفاده کنیم؟

ما زمانی از این معیار فاصله استفاده میکنیم که داده ای با ابعاد بالا داشته باشیم و همچنین دامنه بردارها برای ما اهمیتی نداشته باشد. در تجزیه و تحلیل متن از این معیار خیلی استفاده میشود. برای مثال اگر یک کلمه ای در یک متنی خیلی تکرار میشود این لزوما به این معنی نیست که اون متن مرتبط با اون کلمه است. در چنین حالتهایی استفاده از معیار شباهت کسینوسی میتواند بهترین انتخاب باشد.

فاصله همینگ(Hamming distance)

فاصله همینگ یعنی تعداد مقادیری که در بین دو بردار باهم متفاوت هستند. این معیار معمولا برای مقایسه دو رشته باینری با طول یکسان استفاده می‌شود. همچنین از این معیار برای بررسی شباهت بین دو رشته میتوان استفاده کرد. اینکه چه تعداد از کاراکترهای دو رشته باهم متفاوت هستند.

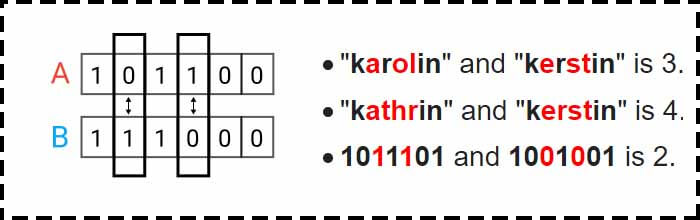
معایب فاصله همینگ (Hamming distance)

همانطور که انتظار می رود، محاسبه فاصله همینگ برای دو برداری که طول یکسانی ندارند سخت هست.  شما از این معیار میتوانید برای بررسی شباهت دو بردار با اندازه یکسان استفاده کنید و متوجه شوید که کدام درایه‌ها باهم یکی نیستند.

علاوه براین، از آنجا که فقط مشخص می‌کند که دو مقدار برابر هستند یا نه، معیار همینگ مقادیر واقعی را برای محاسبه فاصله در نظر نمی گیرد. لذا زمانی که دامنه بردارها برای شما اهیمت دارد، استفاده از این معیار منطقی نیست.

چه زمانی از فاصله همینگ استفاده کنیم؟

استفاده رایج از این معیار در زمانی هست که میخواهید خطا را تصحیح یا شناسایی کنید. موارد استفاده از این معیار شامل تصحیح / تشخیص خطا هنگام انتقال داده از طریق شبکه های رایانه‌ای است. فاصله همینگ میتواند برای تعیین تعداد بیت‌های تحریف شده در یک کلمه باینری به عنوان راهی برای تخمین خطا استفاده شود. علاوه‌براین ، شما همچنین می‌توانید از فاصله Hamming برای اندازه گیری فاصله بین متغیرهای دسته‌بندی استفاده کنید.

فاصله منهتن- بلوک شهری(Manhattan distance)

فاصله منهتن که اغلب به اسم بلوک شهری میشناسیم،برای محاسبه فاصله بین دو برادری که مقادیر واقعی دارد استفاده می‌شود. دو تا برداری را تصور کنید که موقعیت objectها را روی یک شبکه یکنواخت مثل صفحه شطرنج توصیف می‌کنند. اگر بردارها فقط در مسیرهای مستقیم حرکت کنند و امکان حرکت مورب(diagnal) نداشته باشند، در این صورت فاصله منهتن مسافت طی شده بین دو بردار را مشخص می‌کند.

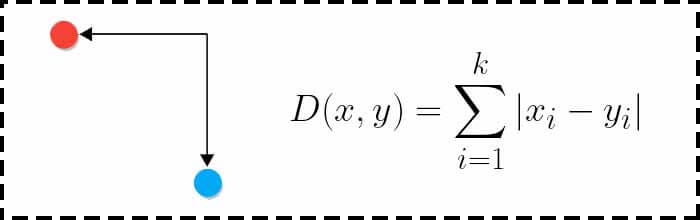
معایب فاصله منهتن (Manhattan distance)

با اینکه به نظر میرسد این معیار در ابعاد بالا خوب عمل کند ولی این معیار نسبت به معیار فاصله اقلیدسی در ابعاد بالا قابل درک(شهودی) نیست . همیچنین این معیار فاصله بیشتری نسبت به اقلیدسی محاسبه می‌کند، چرا که کوتاه‌ترین مسیر را پیدا نمی‌کند. این امر لزوما مشکل آفرین نیست ولی باید به این موضوع آگاه باشیم.

چه زمانی از فاصله منهتن استفاده کنیم؟

هنگامی که مجموعه داده‌های شما دارای ویژگی‌های گسسته و یا باینری باشند، به نظر می‌رسد فاصله منهتن کاملاً خوب کار  کند، زیرا مسیری که به طور واقعی میتوان در مقادیر آن ویژگی‌ها طی کرد،  را در نظر می‌گیرد. در حالی که  مسافت اقلیدسی یک خط مستقیم بین دو بردار بدست می آورد ولی ممکن است این امر امکان پذیر نباشد .

فاصله چبیشف (Chebyshev Distance)

فاصله چبیشف برابر با ماکزیمم اختلاف بین درایه‌های دو بردار است.  به زبان ساده، در این معیار اختلاف تک تک ویژگی‌ها با هم محاسبه شده و سپس ماکزیمم فاصله بین دو ویژگی به عنوان فاصله دو بردار استفاده می‌شود.

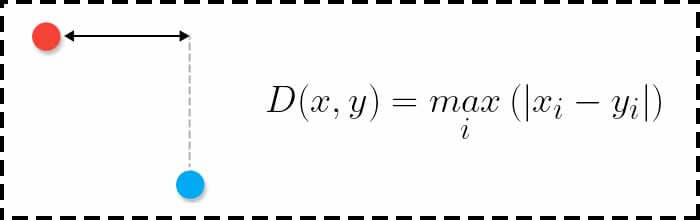
معایب فاصله چبیشف (Chebyshev Distance)

این معیار را تنها میتوان در یک سرای موارد خاص استفاده کرد و نمیتوان از این معیار مثل فاصله اقلیدسی به عنوان یک معیار فاصله همه‌منظوره استفاده کرد.

چه زمانی از فاصله چبیشف استفاده کنیم؟

از این معیار میتوان برای پیدا کردن حداقل تعداد حرکت مورد نیاز از یک میدان به میدان دیگر استفاده کرد. علاوه‌براین، چبیشف می‌تواند معیار مفیدی در بازیهایی باشد که امکان حرکت 8 طرفه بدون محدودیت را دارند.

در عمل، فاصله چبیشف اغلب در انبار کالا استفاده می‌شود زیرا شباهت زیادی به زمانی که جرثقیل سقفی برای جابجایی یک شی سپری می‌کند، دارد.

فاصله مینکوفسکی (Minkowski distance)

فاصله مینکوفسکی مقداری پیچیده تر از اکثر موارد است. معیاری است که در فضای بردار  نرمال شده (فضای واقعی n بعدی) به کار میرود ، به این معنی که می توان از آن در فضایی استفاده کرد که فواصل را می توان به عنوان بردار دارای طول نشان داد.

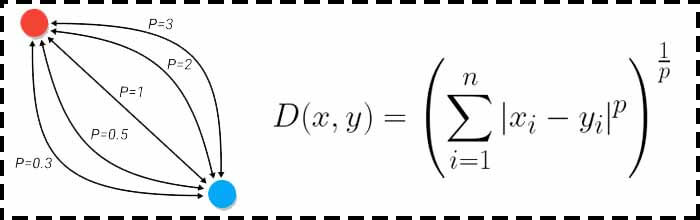
این معیار به سه چیز نیاز دارد:

• بردار صفر: بردار صفر داری طول صفر است درحالی که سایر بردارها طول مثبتی دارند. برای مثال اگر ما از یک مکان به مکانی دیگر سفر کنیم، در آن صورت مسافت طی شده همیشه مثبت است. در حالی که اگر از آن مکان به همان مکان سفر کنیم، در آن صورت فاصله صفر خواهد بود.
• فاکتور اسکالر: اگر شما یک بردار را به یک عدد مثبت ضرب کنید طول آن تغییر می‌کند ولی جهت آن تغییر نمی‌کند. مثلا شما یک مسافتی را در یک جهتی طی کنید، اگر به آن همان فاصله رو اضافه کنید، جهت تغییر نخواهد کرد.
• نابرابری مثلث : کوتاهترین فاصله بین دو نقطه یک خط مستقیم است.

یک چیز بسیار جالب در این معیار استفاده از پارارمتر p است. ما میتونیم با کمک این پارامتر معیار فاصله را تغییر بدهیم. برای مثال اگر p=1 باشد، معیار فاصله به منهتن تبدیل می شود، یا اگر p=2 شود معیار فاصله به اقلیدسی تبدیل می شود و اگر بینهایت باشد در این صورت معیار فاصله به چبشف تبدیل می شود.

معایب فاصله مینکوفسکی

این معیار همان ایراد معیارهای فاصله های ذکر شده را دارد.

چه زمانی از فاصله مینکوفسکی استفاده کنیم؟

مزیت این روش انعطاف پذیری آن است و میتوان با تغییر مقدار p ، معیار مناسب برای مسئله را انتخاب کرد.

شاخص ژاکارد(Jaccard index)

شاخص ژاکارد معیاری است که برای محاسبه شباهت و تنوع نمونه‌های مجموعه استفاده می شود.  فاصله برابر با اندازه اشتراک تقسیم بر اندازه اجتماع نمونه‌های مجموعه است.

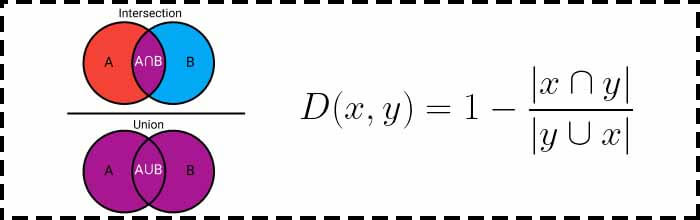
در عمل، تعداد کل نمونه‌های مشابه بین مجموعه‌ها تقسیم بر تعداد کل نمونه‌ها است. به عنوان مثال، اگر دو مجموعه دارای 1 نمونه مشترک باشند و در مجموع 5 نمونه مختلف وجود داشته باشد ، شاخص Jaccard برابر با 1/5=0.2 خواهد بود.

معایب شاخص ژاکارد

مهمترین ایراد شاخص ژاکارد این است که به شدت تحث تاثیر ابعاد داده است. مجموعه داده‌های بزرگ می‌توانند تأثیر بزرگی در شاخص داشته باشند.

چه زمانی از شاخص ژاکارد استفاده کنیم؟

شاخص ژاکارد اغلب در کاربردهایی که داده‌ها باینری یا دودویی هستند استفاده می‌شود  . مثلا زمانی که شما از یادگیری عمیق برای تخمین بخش‌های مختلف یک تصویر استفاده می‌کنید، می‌توان از شاخص Jaccard برای محاسبه دقیق بودن آن بخش پیش‌بینی شده با برچسب‌های واقعی استفاده کرد.

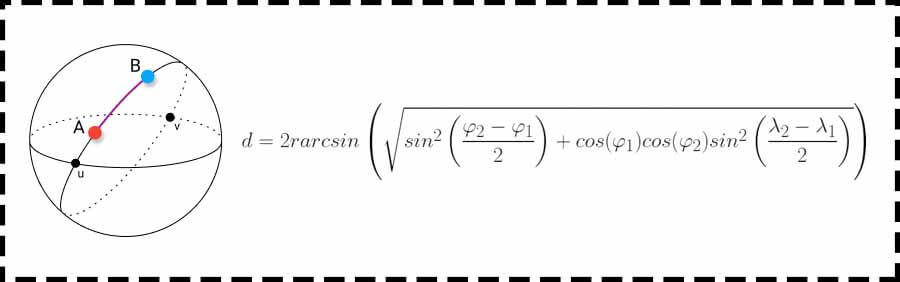
فاصله هاورسین فاصله‌ی بین دو نقطه در روی یک کره با توجه به طول و عرض جغرافیایی آنها است. از آنجا که این فاصله کوتاه‌ترین مسیر بین دو نقطه را پیدا می‌کند، شباهت خیلی زیادی به فاصله اقلیدسی دارد. تفاوت اصلی این است که در اینجا فرض بر این است که دو تا نقطه روی یک کره هستند و فاصله بین دو نقطه یک خط نخواهد بود.

معایب فاصله  Haversine

یکی از عیب‌های این معیار این است که فرض می‌کند نقاط روی یک کره قرا دارند. در عمل، این به ندرت اتفاق می افتد، به عنوان مثال، زمین کاملا گرد نیست و  می‌تواند محاسبه را در موارد خاص دشوار کند.

چه زمانی از شاخص ژاکارد استفاده کنیم؟

همانطور که انتظار میرود این معیار را میتوان در هوانوردی استفاده کرد. برای مثال میتوان از این معیار برای محاسبه فاصله هوایی دو کشور در زمان سفر هوایی استفاه کرد. باید به نکته توجه کنیم که اگر مسیر پرواز دو کشور کوتاه است، این معیار نمی‌تواند معیار مناسبی باشد.

نکته: معیارهای فاصله زیادی وجود دارد. ما در این بخش به 8 تا از معیارها اشاره کردیم. معیارهای زیادی مثل ماهالانوبیس، کورولیشن و … نیز وجود دارد. اگر از الگوریتمهایی استفاده میکنید که در آنها از معیار فاصله استفاده می شود حتما به این نکته توجه کنید و سعی کنید معیارهای مختلف را برای مسئله استفاده کنید. چرا که معیار فاصله دقت الگوریتم را بسیار تحت تاثیر قرار میدهند و به نوعی عملکرد الگوریتم وابستگی بسیار زیادی به نوع معیار دارد.

ما در فصل چهارم دوره جامع شناسایی الگو -یادگیری ماشین معیارهای زیادی برای پیاده‌سازی knn استفاده کرده ایم و با آزمایش های مختلف نشان داده ایم که در هر پایگاه داده ای معیار فاصله تاثیر به سزایی در نتیجه عملکرد الگوریتم دارد. پینشهاد میکنیم این فصل را مشاهده کنید.