ماشین بردار پشتیبان svm
ماشین بردار پشتبیان(svm) یکی از طبقهبندهای معروف در حوزه شناسایی الگو جهت دسته بندی دادهها است. طبقهبند svm پایه ثابت اکثر مقالات تخصصی است و می بینیم که از طبقهبند svm برای طبقه بندی در اکثر کارها استفاده میکنند. در این بخش میخواهیم بررسی کنیم که طبقه بند svm در مسائل طبقه بندی خطی و غیرخطی چه رویکردی دارد و به چه شکل طبقه بندی را انجام می دهد که باعث شده بین محققین این همه محبوب باشد.
ماشین بردار پشتیبان (svm)
ماشین بردار پشتیبان(support vector machine) توسط آقای ولادیمر وپنیک(Vapnik ) در سال 1995 با عنوان support vector networks برای طبقه بندی داده های دو کلاسه خطی مطرح شد. که بعدا توسط Vapnik برای مسائل غیرخطی و چندکلاسه توسعه پیدا کرد. این الگوریتم خیلی سریع مورد توجه محقققن قرار گرفت و از میزان سایتیشن این مقاله میتوان متوجه شد که چقدر میان محقیق محبوب است!

در ابتدا دلایل محبوبیت svm را مطرح میکنیم و سپس رویکرد کلی ارائه شده را به صورت مختصر بیان میکنیم.
در مسئله بهینه سازی svm به طور صریح و واضح مشخص شده که بهترین مرز پیدا شود!
یکی ازمهترین مزیت svm این است که در مسئله بهینه سازی این الگوریتم، آقای Vapnik یک مسئله بهنیه سازی جهت پیدا کردن مرز تعریف کرده که در آن به طور صریح مشخص شده است که بهینه ترین مرز بهینه پیدا شود! این در حالی هست که در سایر الگوریتم ها مثل شبکه عصبی با اینکه دنبال مرز بهینه هستند، ولی در مسئله بهینه سازی آنها هیچ قید و شرطی جهت رسیدن به بهنیه ترین مرز ممکن اعمال نشده است.
آقای Vapnik همراه با تابع هزینه قیدی هم در نظر گرفته است و این قید مسئله بهینه سازی را مجبور میکند که دنبال بهینه ترین مرز باشد. و اگر مسئله طبقه بندی داری جواب باشد، به عبارتی امکان پیدا کردن مرز بهینه ای باشد، الگوریتم به بهینه ترین مرز ممکن همگرا میشود.
مسئله بهینه سازی svm محدب هست و همین باعث میشود که در مینیمم محلی گیر نکند!
برای حل مسئله طبقه بندی میتوان گفت که جوابهای مختلفی وجود دارد، به عبارتی برای تفکیک داده های دو گروه میتوان بی نهایت مرز تفکیک کننده پیدا کرد. ولی بین این مرزها، یک مرزی وجود دارد که بهینه ترین مرز ممکن برای تفکیک داده های دو گروه هست.
مزیت دوم svm این است که مسئله بهینه سازی آن یک مسئله بهینه سازی محدب (concave) هست و این باعث میشود که الگوریتم در مینیمم های محلی(local minima ) گیر نکند. و اگر مسئله دارای جواب باشد، الگوریتم svm به بهینه ترین جواب همگرا میشود. به عبارتی الگوریتم svm بهترین مرز تفکیک کننده داده های دو گروه را پیدا میکند
svm در ابعاد بالا هم خیلی خوب عمل میکند!
طبقه بند svm به طور صریح و مشخص دنبال پیدا کردن بهترین مرز ممکن در مسائل طبقه بندی هست. به خاطر اینکه برای پیدا کردن مرز بهینه از بردارهای پشتیبان کمک میگیرد، باعث میشود در ابعاد بالا هم خیلی خوب عمل میکند و این یکی از مهمترین دلایل محبوبیت svm است.
مرز تصمیم گیری svm
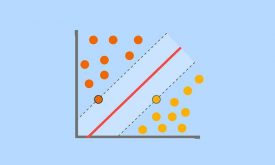
مرز تصمیم گیری باید طوری بدست بیاید که در پروسه تست هنگام مواجه شدن با داده های جدید نیز خوب عمل کند. چنین مرزی بهتر است که بیشترین حاشیه را نسبت به داده های دو گروه داشته باشد. چون در عمل داده های جدید تغییرات نسبی نسبت به داده آموزش خواهند داشت. در اینصورت اگر مرز حاشیه زیادی داشته باشد، احتمال خطای کمتری خواهد داشتو در داده های جدید هم خوب خواهد بود.
svm دنبال مرزی هست که علاوه بر جدا کردن داده های دوگروه، بیشترین فاصله را نسبت به نزدیکترین داده های دو گروه داشته باشد. به نزدیکترین داده های هر گروه نسبت به مرز تصمیم گیری را بردارهای پشتیبان میگوییم. مرز تصمیم گیری svm بیشترین حاشیه(margin) را دارد و همین باعث میشود، در داده های جدید که تغییرات نسبی نسبت به داده آموزش دارند، نیز خوب عمل کند.
ماشین بردار پشتیبان در مسائل خطی تفکیک پذیر(hard margin svm)
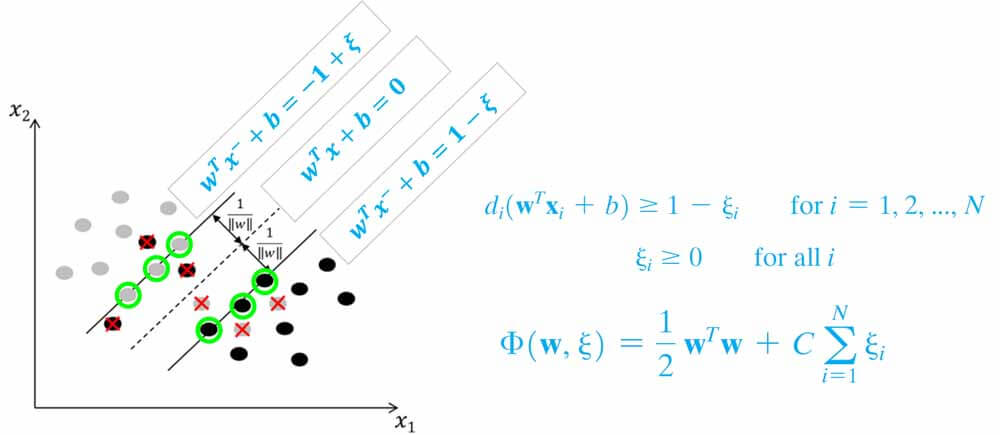
فرض کنید یک دو مسئله دو کلاسه برای طبقه بندی دارید، که در آن داده های دو کلاس به صورت خطی کاملا تفکیک پذیر هستند. برای پیدا کردن مرز تفکیک کننده چنین داده ای، آقای Vapnik چنین مسئله بهینه سازی تعریف کرده اند:
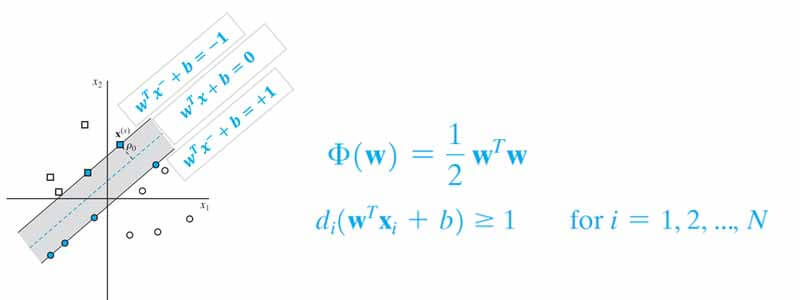
در این مسئله هدف svm این است مرزی پیدا کند تا نه تنها داده های دو گروه را به درستی دسته بندی کند، بلکه بیشترین فاصله را نیز نسبت به نزدیک ترین نمونه های هر کلاس داشته باشد.
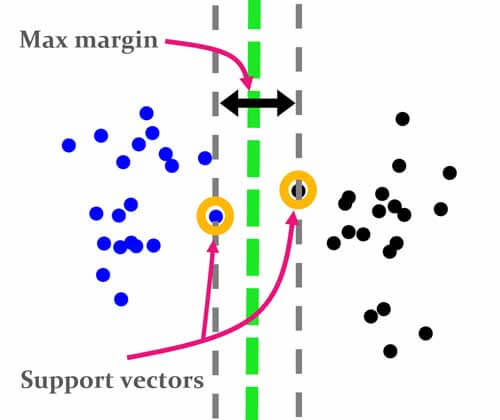
در hard margin svm هدف این است که در حاشیه نمونهای از دادههای دو گروه نباشد. به عبارت دیگر دقت طبقهبندی روی داده آموزش 100 درصد باشد.
در این حالت انگار svm یک فنری دارد که وسط داده ها باز میکند و این فنر تا جایی که نمونه ای وجود نداشته باشد کش پیدا میکند و در نهایت که از هر دو طرف چسبید به نزدیکترین نمونه های هر کلاس(بردارهای پشتیبان) میایسته و مرز بهینه بدست می آید.
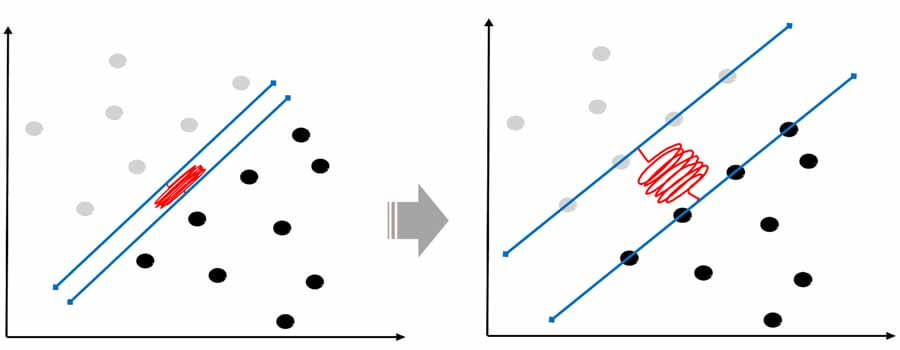
ماشین بردار پشتیبان در مسائل خطی تفیک ناپذیر(soft margin svm)
مطئمنا در واقعیت، داده ها انقدر تمیز نیستند و ممکن است داده ها با آنکه به صورت خطی تفکیک پذیر هستند، ولی تو هم رفته اند و کاملا تفکیک شده نباشند.
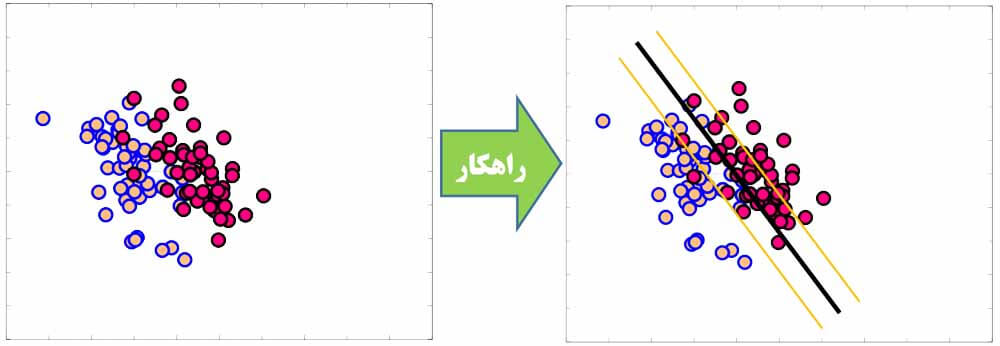
یا حتی داده ها تفکیک پذیر باشند، ولی اگر دنبال مرزی باشیم که در حاشیه آن نمونه ای وجود نداشته باشیم، به مرز بهتری منجر نشود.
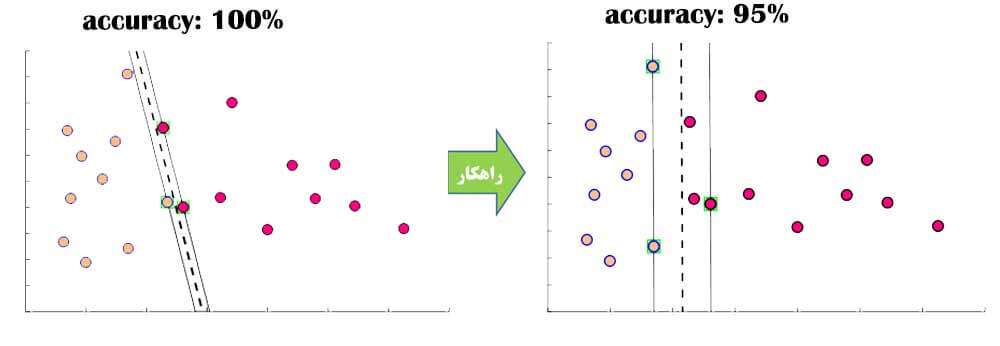
در چنین مسائلی آقای Vapnik به جای اینکه دنبال مرزی باشد که به دقت 100 درصد منجر شود، مسئله بهنیه سازی را تعمیم داده و از یک متغیر مجازی(slack variable) کمک میگیرد تا الگوریتم svm دنبال مرزی باشد که کمترین خطای دسته بندی داشته باشد. ولی همچنان خاصیت قبل را داشته باشد، یعنی بیشترین فاصله را داشته باشد.
برای اینکار با مسئله را اینطور در نظر میگیرد که در حاشیه تعدادی از نمونه های دو گروه قرار بگیرید. با اینکار به الگوریتم این آزادی را میدهد که مرز را در جایی قرار دهد که بهتر است ولی ممکن است دقت طبقه بندی کمتر از 100 باشد.
ماشین بردار پشتیبان در مسائل غیر خطی(nonlinear svm)
مسئله بهنیه سازی ارائه شده توسط آقای Vapnik برای مسائل خطی است و این مسئله را نمیتوان مستقیما برای مسائل طبقه بندی غیر خطی استفاده کرد.
آقای Vapnik برای حل این مسئله هم از یک قضیه بسیار جالب به اسم کاور کمک میگیرد. تئوری کاور بیان میکند که اگر داده ای داشته باشیم که به صورت غیرخطی تفکیک پذیر باشد، میتوان با یک تبدیل غیرخطی از فضای غیرخطی به فضای خطی نگاشت داد. که در این فضا داده ها به صورت خطی تفکیک پذیر می شوند.
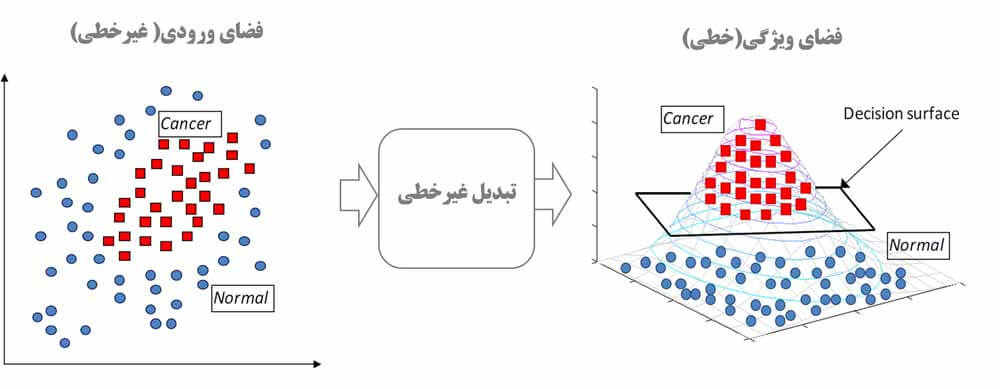
آقای Vapnik برای نگاشت داده ها از فضای غیرخطی به فضای خطی، ویژگی ها را به صورت غیرخطی باهم ترکیب می کند و یک سری ویژگی هایی می سازد که داده توسط این ویژگی ها به صورت خطی تفکیک پذیر میشود و حال میتوان همان مسئله بهینه سازی مسائل خطی را در این فضا برای پیدا کردن مرز بدست آورد. مرز خطی که در فضای جدید(فضای ویژگی) بدست می آید معادل همان مرز غیرخطی در فضای اصلی است!
برای ترکیب غیرخطی ویژگی ها هم کرنالهای مختلفی مثل کرنل rbf، کرنل polynomial، کرنل quadratic و غیره میتوان استفاده کرد.
اگر علاقه مند به یادگیری تخصصی و پیادهسازی گام به گام svm هستید به دوره جامع شناسایی الگو و یادگیری ماشین مراجعه کنید. در فصل چهارم این دوره، تئوری و ریاضیات الگوریتم svm از پایه به صورت تخصصی آموزش داده شده و سپس گام به گام پیاده سازی شده است. در انتها هم چندین پروژه عملی در مسائل طبقه بندی و رگرسیون با الگوریتم svm انجام شده است.
در پست بعدی ماشین بردار پشتیبان در مسائل رگرسیون رو توضیح خواهیم داد.
hard margin svm
soft margin svm





[…] که بیشترین فاصله را به نزدیکترین نمونه های هر گروه (بردارهای پشتیبان) داشته […]
عالی بود
ممنون از لطف شما