رگرسیون با ماشین بردار پشتیبان SVR

چندتا از مزیتهای ماشین بردار پشتیبان

• مسئله بهینه سازی SVM محدب هست و همین باعث می شود که در حل مسئله اگر جوابی وجود داشته باشد به بهینه ترین جواب ممکن همگرا شود. یعنی در مسائل طبقه بندی بهترین مرز تفکیک کننده ممکن بین دو گروه را پیدا میکند.
• در مسئله بهینه سازی SVM به طور صریح قیدی تعریف شده است که مرز بدست آمده بیشترین فاصله را با داده های دو گروه داشته باشد، و این قید کمک میکند که احتمال خطای تصمیم گیری SVM در شرایط واقعی بسیار کم باشد.
• از طرفی چون SVM مرز را براساس بردارهای پشتیبان بدست می آورد، در ابعاد بالا هم خوب عمل می‌کند.

اگر بتوان براساس همین مزیت های SVM یک مدلی برای مسائل رگرسیون طراحی کرد، مطمئنا عملکرد خیلی خوبی خواهد داشت. چرا که همین مزیت های SVM در مسائل طبقه بندی باعث شده که عملکرد بسیار خوبی نسبت با سایر طبقه بندها داشته باشد.

در ادامه توضیح میدهیم که چطور میتوان از ماشین بردار پشتیبان برای مسائل رگرسیون استفاده کرد. از آنجا که درک رویکرد ماشین بردار پشتیبان در مسائل طبقه بندی ساده تر هست برای همین توضیحات SVR در مسائل رگرسیون را همراه با رویکرد SVM در مسائل طبقه بندی بیان می کنیم.

فرق بین مسئله طبقه بندی و رگرسیون

کلاسبندی و رگرسیون هر دو جزء دسته یادگیری با ناظر هستند که هدفشان پیدا کردن رابطه بین ورودی و خروجی است. به طور کلی در یادگیری نظارت شده، ما مدل را با استفاده از یک سری داده‌هایی که از قبل خروجی مطلوب (مقادیر پیوسته یا گسسته) آنها مشخص شده است، آموزش میدهیم و هدف این است که وقتی یک داده جدید  که خروجی آن مشخص نیست به مدل ارائه شد، مدل بتواند خروجی مطلوب را تولید کند.

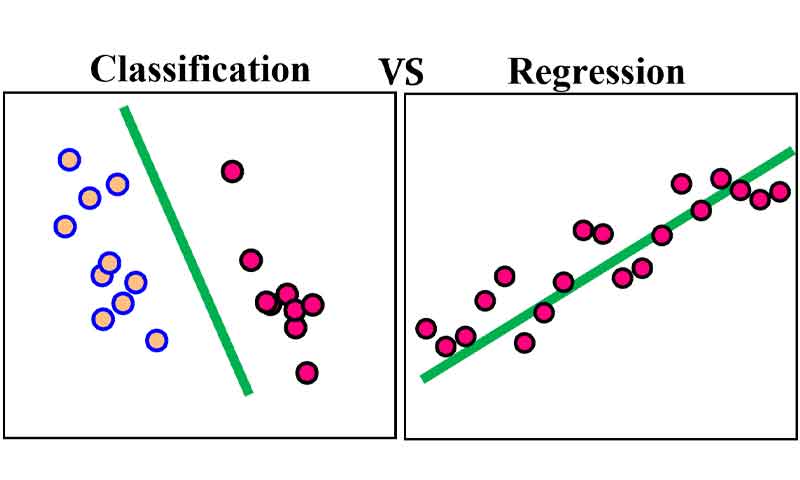
برای جزئیات بیشتر به  تفاوت بین رگرسیون و طبقه بندی مراجعه کنید. در یک پست جداگانه این مسئله را کامل توضیح داده ایم.

SVM در مسائل خطی تفکیک‌پذیر (طبقه بندی)

فرض کنید یک مسئله طبقه بندی دو کلاسه ای داریم که در آن داده های دو کلاس به صورت خطی کاملا تفکیک پذیر هستند، در این صورت SVM دنبال مرزی هست که اولا خطای صفر را داشته باشد، دوما مرزی بدست آورد که بیشترین فاصله را به نزدیکترین نمونه های هر گروه (بردارهای پشتیبان) داشته باشد.

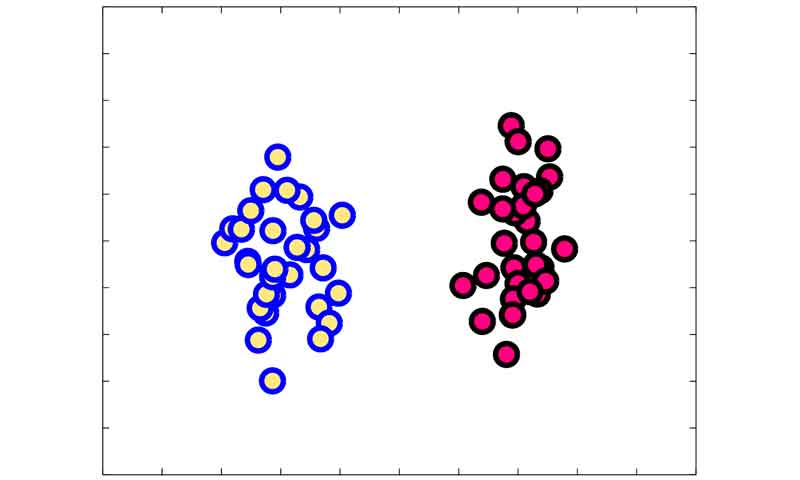
برای رسیدن به چنین هدفی SVM از مسئله بهینه سازی زیر استفاده میکند:

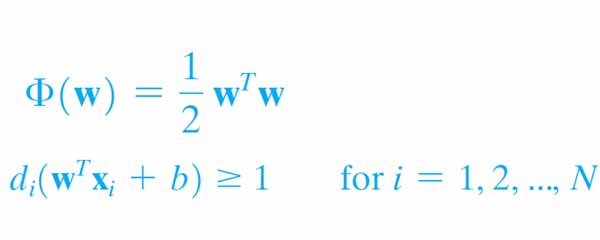
در این مسئله بهینه سازی ذکر شده است که مرزی بدست بیاید که بیشترین Margin را داشته باشید و همچنین قیدی وجود دارد که مجبور میکند مدل مرزی پیدا کند که تصمیم گیری درستی انجام بدهد. با چنین تابع هزینه و قیدهایی SVM در مسائل طبقه بندی خطی تفکیک پذیر بهترین مرز ممکن بین دو گروه را پیدا میکند.

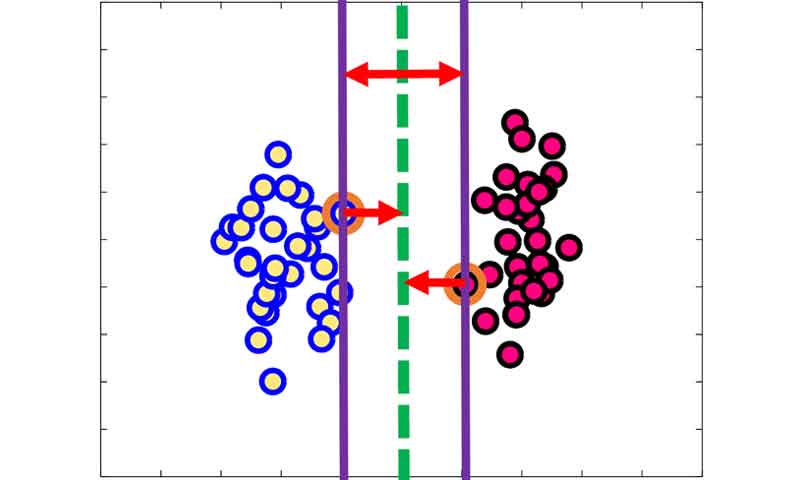
در چنین مسئله ای svm دنبال مرزی هست که در margin آن هیچ نمونه ی آموزشی نباشد (ساده‌تر بگم، خالی از سکنه باشه)! با این رویکرد حاشیه امنیت خوبی ایجاد می‌کند و تضمین می‌کند تا در شرایط واقعی که داده های جدید تغییراتی نسبت به داده های آموزش دارند، همچنان خوب عمل کند. چون در اینصورت اکثر نمونه های تست در مارجین قرار میگیرند و احتمال خطای تصمیم گیری خیلی کاهش می یابد.

 

SVR در مسائل خطی بدون outlier (رگرسیون)

در مسائل رگرسیون ما دنبال رابطه بین ورودی و خروجی هستیم . که این رابطه میتواند خطی و یا غیرخطی باشد. فعلا فرض کنیم که رابطه بین ورودی و خروجی یک رابطه خطی هست و میخواهیم بهترین رابطه خطی بین ورودی و خروجی را بدست بیاوریم. شبیه مسئله خطی طبقه بندی، میتوانیم یک مسئله رگرسیون خطی داشته باشیم که در آن خروجی داده ها همه رفتار خطی داشته باشند، یعنی همه همانند شکل زیر در اطراف یک خط باشند و خروجی هیچ نمونه ای فاصله ی زیاد و غیرمعقولی با خط نداشته باشد.

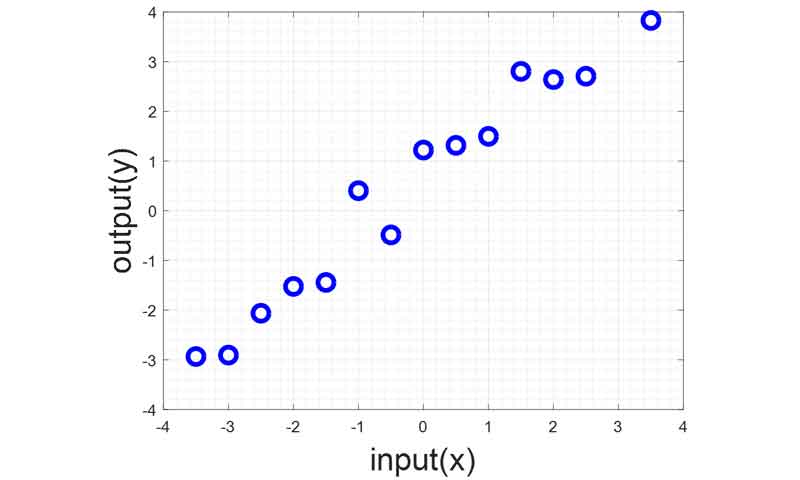
در چنین حالتی SVR دنبال رابطه خطی هست که از وسط خروجی ها عبور کند، و مارجینی داشته باشد که در آن خروجی همه نمونه ها در داخل مارجین قرار بگیرند. با چنین رویکردی میتوان بهترین رابطه خطی ممکن بین ورودی و خروجی بدست آورد.

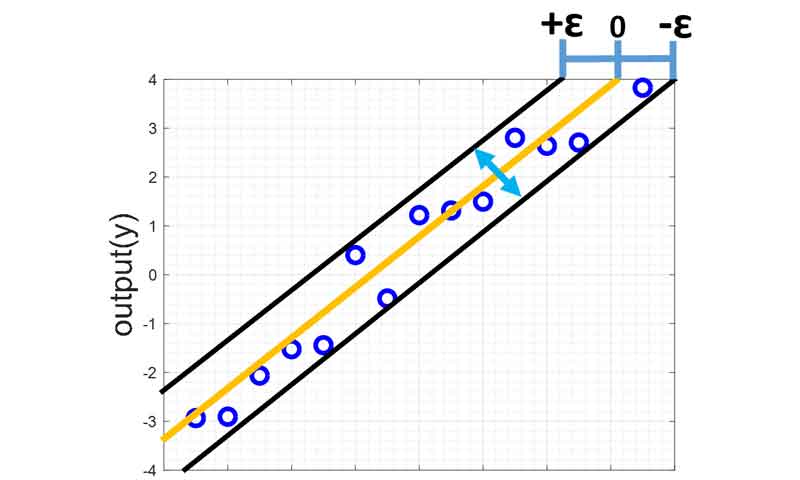
در مسائل خطی تفکیک پذیر SVM دنبال مرزی است که در مارجین آن هیچ نمونه ای نباشد(خالی از سکنه باشد)، اما SVR در مسائل خطی بدون outlier دنبال خطی هست که در مارجین آن همه نمونه‌ها قرار بگیرند! همه نمونه ها! بدون هیچ استثنایی!چون لازمه بدست آوردن بهینه ترین رابطه خطی ممکن بین ورودی و خروجی در مسائل خطی بدون outlier  داشتن چنین مارجینی هست!

برای چنین کاری SVR از تابع هزینه زیر استفاده می کند:

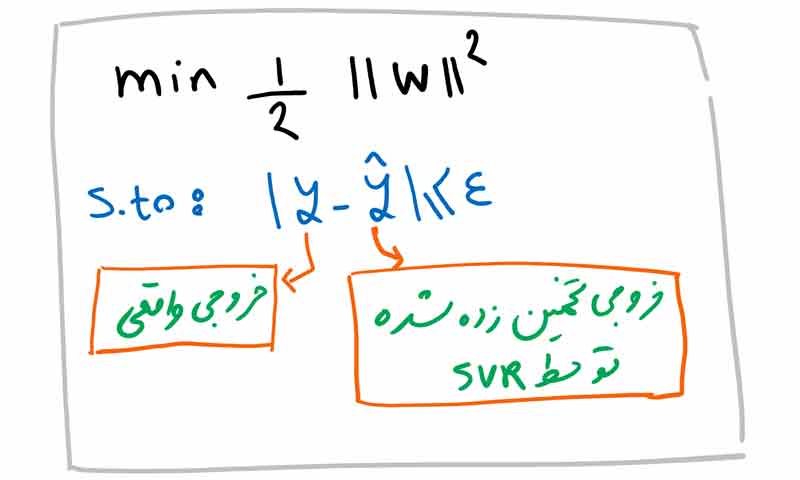
SVM در مسائل خطی تفکیک ناپذیر (طبقه بندی)

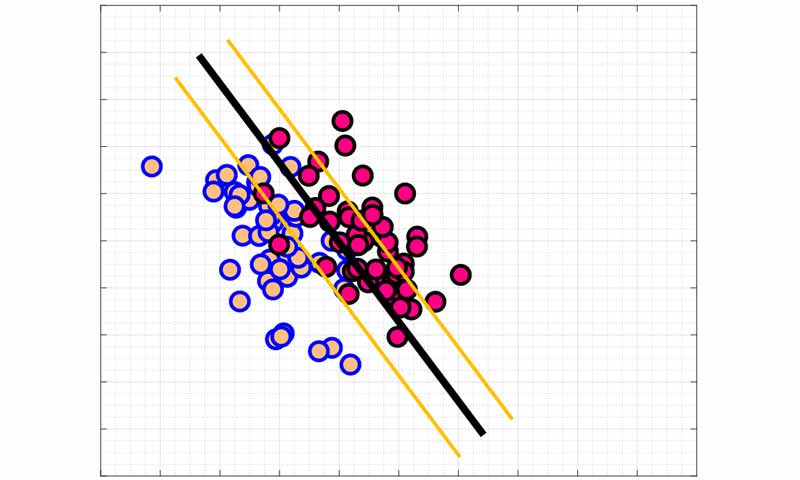
مشکلی که تابع هزینه قبلی SVM دارد این است که اگر طبق شکل زیر داده های آموزش کاملا خطی تفکیک پذیر نباشند، امکان بدست آوردن مرزی که خطای صفر داشته باشد وجود ندارد.

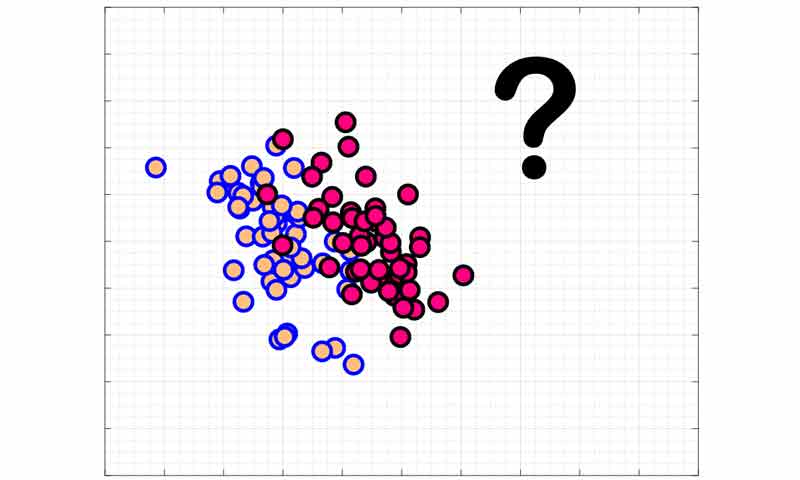
همانطور که در شکل میبینیم با اینکه داده ها کاملا با یک خط تفکیک پذیر نمی‌‎شوند ولی همچنان میتوان یک مرزی بدست آورد که حداقل خطا را داشته باشد. برای حل این مشکل Vapnik از متغیر مجازی (slack variable) استفاده میکند و با این رویکرد به مدل امکان یک خطای حداقل میدهد.

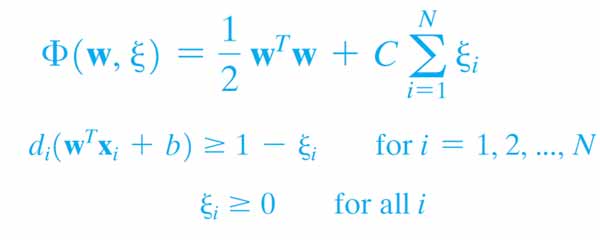
نقش متغیر مجازی (slack variable) در تابع هزینه این است که به مسئله بهینه سازی اجازه دهد چندین نمونه در مارجین قرار بگیرند.در حالی که در رویکرد اول به هیچ عنوان  چنین اجازه ای داده نمی شد و مارجین باید خالی از سکنه می بود. اینکه چه میزان از نمونه ها در مارجین قرار بگیرند بستگی به مسئله دارد و توسط کاربر تعیین می شود.

SVR در مسائل خطی همراه با outlier (رگرسیون)

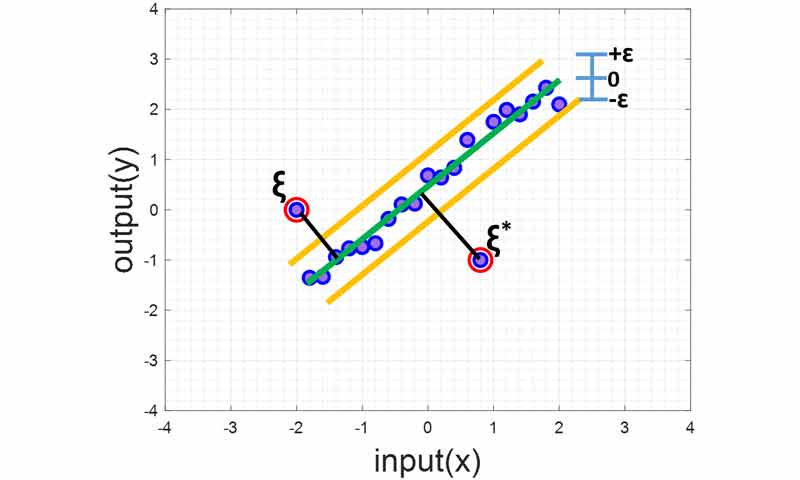
همانند مسئله خطی تفکیک ناپذیر در مسائل طبقه بندی، در مسائل رگرسیون نیز همانند شکل زیر ممکن است خروجی داده‌ها یک رفتار خطی داشته باشند، ولی برخی از خروجی ها outlier باشند، یعنی نمونه هایی وجود داشته باشد که خروجی آنها مقدار خیلی متفاوتی با سایر خروجی ها داشته باشد و  از خط بین نمونه‌ها فاصله خیلی زیادی داشته باشد. به این نمونه ها outlier میگوییم.

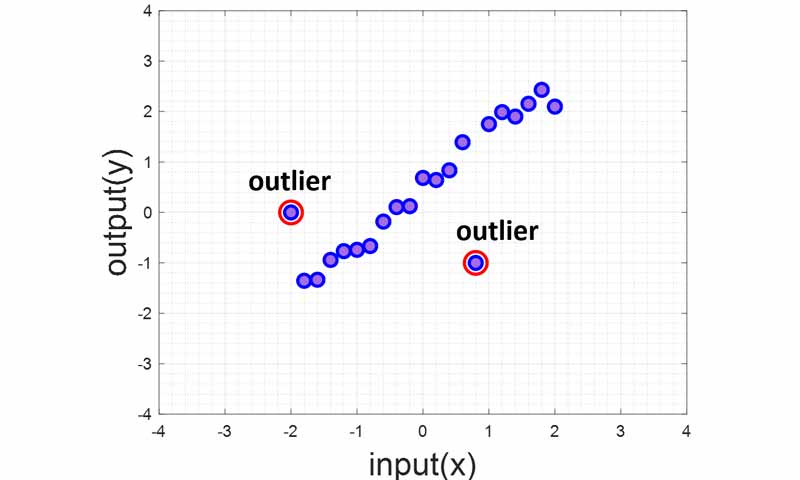
اگر طبق رویکرد اول SVR عمل کنیم و رابطه ی خطی پیدا کنیم که در آن مارجین طوری بدست بیاید که خروجی همه نمونه ها حتی outlierها در مارجین باشند، در این صورت رابطه خطی مناسبی برای رگرسیون بدست نخواهد آمد. چرا که outlier ها تاثیر منفی خود را خواهند گذاشت.

برای حل این مسئله SVR نیز از رویکرد SVM استفاده میکند و به تابع هزینه یک متغیر مجازی اضافه میکند تا بتواند مشکل Outlier ها را حل کند.

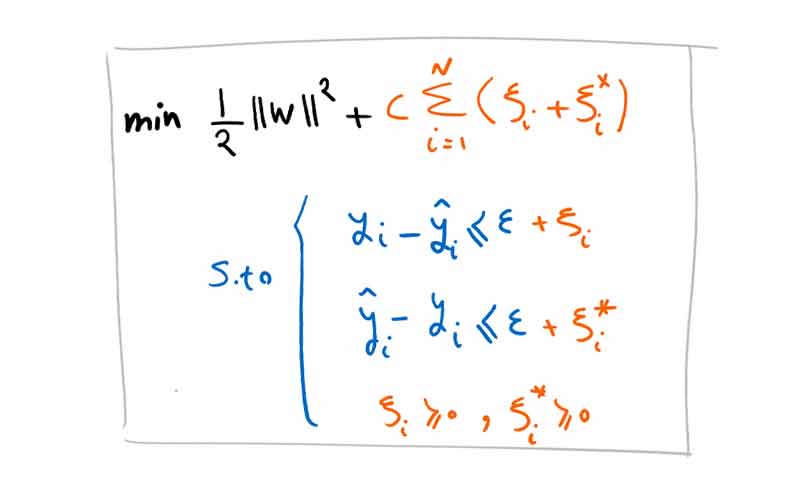
متغیر مجازی(slack variable) در مسائل طبقه بندی خطی به SVM این اجازه را می دهد که چندتا از نمونه ها در مارجین قرار بگیرند، و دار مسائل رگرسیون به SVR این اجازه را میدهد که چندین نمونه خارج از مارجین قرار بگیرند. و با اینکار اثر Outlier ها را خنثی می کند. به عبارتی outlierها را ignore میکند!

SVM در مسائل غیرخطی (طبقه بندی)

در ابتدا Svm برای مثال خطی ارائه شده بود که بعد برای مسائل غیرخطی تعمیم داده شد. Vapnik برای طبقه بندی داده های غیرخطی از نگاشت غیرخطی کمک گرفت.

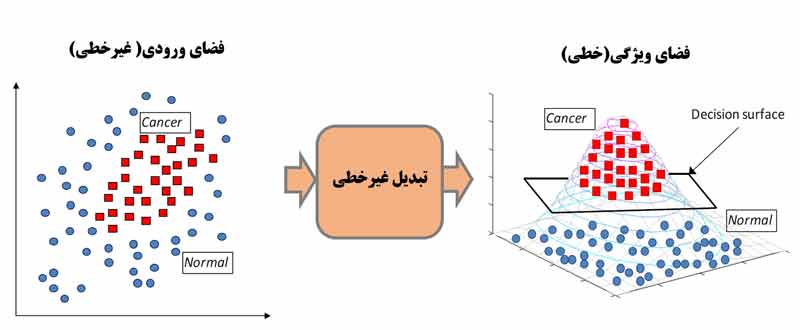
در این رویکرد، در ابتدا داده ها توسط یک نگاشت غیرخطی به فضای خطی نگاشت پیدا میکنند، و سپس در فضای جدید خطی مرز خطی بهنیه بدست می آید، که این مرز معادل مرز غیرخطی بهینه در فضای غیرخطی است.

SVR در مسائل غیرخطی (رگرسیون)

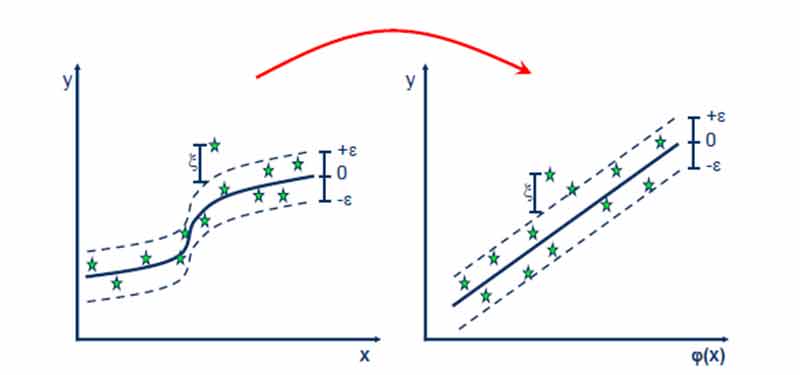
جهت تعمیم SVR برای حل مسائل غیرخطی نیز از چنین رویکردی استفاده می شود. یعنی در ابتدا داده ها با کمک یک نگاشت غیرخطی به فضای خطی نگاشت پیدا می‌کنند، و سپس در فضای جدید رابطه خطی بین داده ها در فضای ویژگی و خروجی بدست می آید. که این رابطه خطی در فضای ویژگی معادل رابطه غیرخطی بین ورودی و خروجی در فضای اصلی است.

در فصل 4 دوره جامع شناسایی الگو-یادگیری ماشین تئوری و ریاضیات ماشین بردار پشتیبان در مسائل طبقه بندی و رگرسیون به طور کامل  آموزش داده شده و سپس به طور مرحله به مرحله پیاده سازی شده است. برای درک بهتر رویکرد ماشین بردار پشتیبان در ابتدا مسائل بسیار ساده استفاده شده است، سپس چندین پروژه عملی در مسائل طبقه بندی و رگرسیون انجام شده است تا با چالشهای انجام پروژه های عملی با ماشین بردار پشتیبان آشنا شوید.