تست آماری ttest و مفهوم p-value

تست آماری ttest  یا anova جزء روشهایی هستند که براساس یک فرضیه آماری انتخابِ ویژگی را انجام میدهند. تست آماری ttest یک روش انتخاب ویژگی اسکالر است که  براساس یک فرضیه آماری به تک تک ویژگی‌ها  یک pvalue اختصاص می‌دهد و سپس براساس مقدار pvalue ، ویژگی های مناسب را انتخاب می‌کند.

روشهای انتخاب ویژگی اسکالر تک تک ویژگی‌ها را به صورت جدا بررسی کرده و براساس میزان تفکیک پذیری به آنها یک امتیازی اختصاص می‌دهند و سپس براساس امتیاز ویژگی‌ها، بهترین ها را انتخاب میکنند.

اساسا هدف روشهای مبتنی بر فرضیه‌های آماری این است که میزان تفکیک‌پذیری یک ویژگی را بررسی کرده و میزان معنادار بودن آن را مشخص کنند. در این روشها براساس میزان معنادار بودن تفکیک‌پذیری یک ویژگی به آن یک امتیازی اختصاص می‌دهند که بعدا میتوان براساس این امتیاز ویژگی‌های مناسب را انتخاب کرد.

مفهوم معنادار بودن تفکیک پذیری یک ویژگی

فرض کنید در یک مسئله ی دو کلاسه 3 تا ویژگی استخراج کرده اید و توزیع آماری هر کدام از ویژگی در داده های  دو کلاس به صورت زیر است.

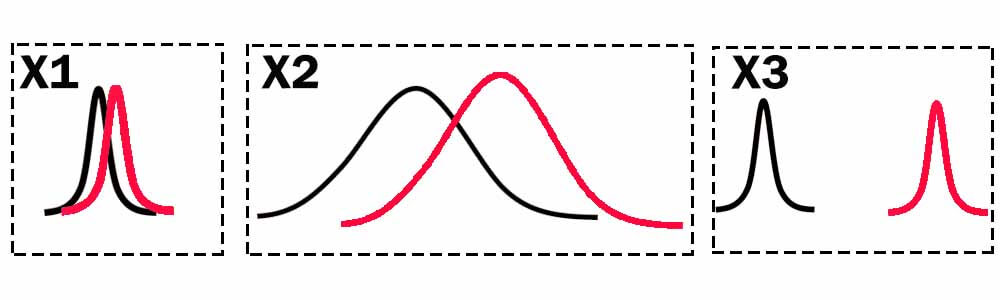
اگر بنا باشد یکی از این ویژگی ها را انتخاب کنیم، به نظر شما کدام ویژگی مناسب است؟ به عبارتی با داشتن کدام ویژگی میتوانیم داده های دو کلاس را با دقت بالایی از هم تفکیک کنیم؟

مطمئنا همه ویژگی 3 را انتخاب میکنند! چرا؟ به خاطر اینکه داده‌های دو کلاس توسط این ویژگی کاملا تفکیک شده اند و ویژگی سوم مقدار کاملا متفاوتی در بین داده های دو کلاس دارد . ویژگی سوم تفکیک پذیری بالایی است یا به عبارتی میزان تفکیک‌پذیری این ویژگی در داده‌های دو گروه معنادار است.

در مقایسه با سایر ویژگی‌ها اختلاف میانگین ویژگی در داده‌های دوگروه زیاد است و میزان پراکندگی داده‌های هر کلاس کم است. ویژگی‌ای که میزان تفکیک پذیری معناداری دارد، واریانس درون کلاسی حداقل و واریانس بین کلاسی حداکثر دارد.

برای مثال، در مسئله ماهی سالمون و سیباس، طول همه ماهی سالمون بین 9-11 و طول همه ماهی های سیباس بین 99 -101 باشد! در چنین حالتی خیلی راحت میتوان ماهی‌های سالمون و سیباس را از هم تفکیک کرد! دلیلش این است که میزان تفکیک پذیری ویژگی طول در دو گروه معنادار است.

فرضیه‌های آماری

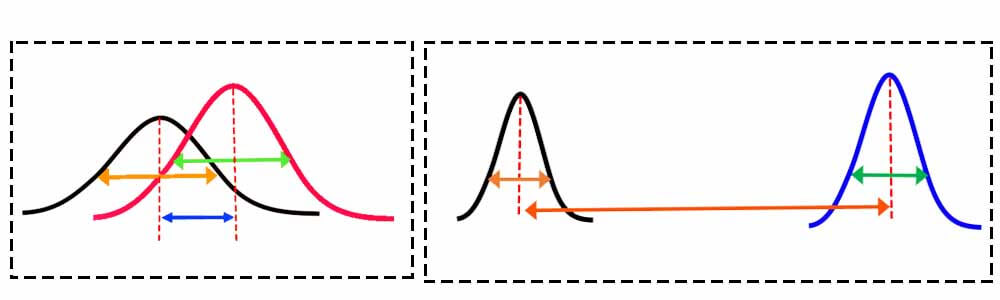
در روشهای مبتنی بر فرضیه های آماری دو تا فرضیه خنثی(null) و مقابل(alternative ) وجود دارد. فرضیه null زمانی پذیرفته می‌شود که اختلاف بین میانگین‌ها معنادار نباشد. به عبارتی ویژگی تفکیک پذیر نباشد. در اینصورت ویژگی برای تفکیک داده‌های دو کلاس مناسب نخواهد بود.

فرضیه alternative زمانی پذیرفته می شود که اختلاف بین میانگینها معنادار باشد. به عبارتی ویژگی برای تفکیک داده‌های دو کلاس مناسب باشد. در اینصورت میتوان با کمک این ویژگی داده های دو کلاس با دقت بالایی از هم تفکیک کرد.

 فرض کنید یک محقق دو گروه از افراد یک جامعه را مورد مطالعه قرار داده است، گروه اول افرادی ورزشکار هستند و گروه دوم افرادی هستند که خیلی کم ورزش می‌کنند.برای مطالعه 300 نفر از افراد ورزشکار جامعه و 300 نفر از افراد غیر ورزشکار جامعه را به صورت کاملا تصادفی انتخاب کرده است.

هدف محقق بررسی ارتباط بین ورزش و فشار خون افراد است. برای همین فشار خون هر دو گروه را اندازه گیری کرده است. حال محقق میخواهد بداند که آیا تفاوتی بین فشار خون افراد ورزشکار و افرادی که ورزش نمی‌کنند وجود دارد؟ و اگر تفاوتی وجود دارد این تفاوت چقدر معنادار است؟! فرض کنید توزیع فشار خون در دو گروه به این شکل است. میانگین فشارخون گروه ورزشکار8 و گروه غیر ورزشکار 10 است. یک اختلافی بین فشار خون دو گروه وجود دارد.

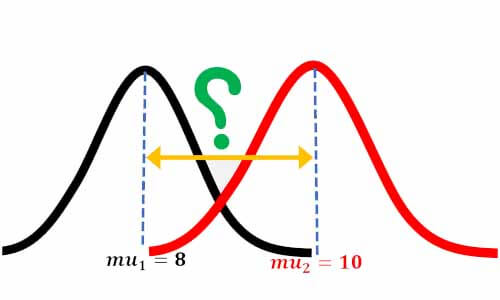
سوال این است که آیا این محقق براساس چنین مشاهده‌ای میتواند قضاوت کند که فشار خون در افراد ورزشکار و غیرورزشکار متفاوت است؟ آیا مشاهده‌ی محقق یک fact علمی است و ورزش روی فشار خون افراد تاثیر میگذارد یا به خاطر یک فرایند تصادفی همچین نتیجه‌ای مشاهده شده است؟ اگر دوباره این آزمایش را محقق روی افراد جدید انجام دهد همچین اختلافی را مشاهده خواهد کرد؟ محقق چطور میتواند علمی بودن این مسئله را بررسی کند؟

اینجاست که ttest به کمک محقق می آید و مشخص می‌کند که نتیجه مشاهده شده یک واقعیت عملی است یا به خاطر یک فرایند تصادفی ایجاد شده است.

روش آماری ttest

روش آماری ttest در ابتدا یک مقدار کمی برای نشان دادن میزان اختلاف میانگین دو گروه بدست می آورد. این مقدار tvalue است. که براساس میانگین و استاندارد erorr   ویژگی در دو گروه بدست می آید(در یک جلسه جدا در مورد این مسئله صحبت خواهیم کرد. فعلا این رو همان انحراف معیار (میزان پراکندگی حول میانگین) در نظر بگیرید)

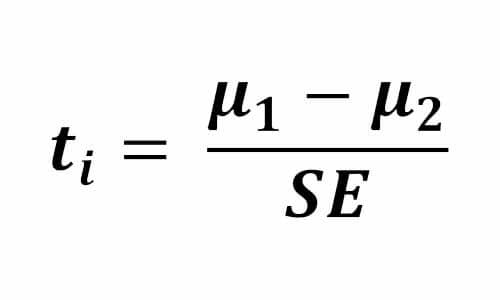
اگر از دید انتخاب ویژگی هم به مسئله نگاه کنیم tvalue پارامتر مناسبی برای بررسی تفکیک‌پذیری یک ویژگی هست. چرا که براساس اختلاف بین میانگین‌ها  و واریانس دورن کلاسی نوشته شده است. و هرچقدر tvalue بیشتر باشد ویژگی تفکیک‌پذیری زیادی خواهد داشت.

مفهوم pvalue

فرض کنید tvalue برابر با 4 شده است. الان معنی این عدد چیه؟ عدد بزرگی است یا کوچک؟ آیا الان میتوانیم قضاوت کنیم که ورزش کردن روی فشار خون افراد تاثیر مستقیمی دارد یا نه؟ خیر! چون مقدار tvalue فقط اختلاف میانگین دو گروه را مشخص میکند. ولی اینکه این اختلاف معنادار است یا نه را نمی توان به طور مستقیم از روی عدد بدست آمده برای tvalue متوجه شد. راه چاره چیه؟ الان از کجا متوجه شویم که مقدار بدست آماده برای tvalue نشان دهنده اختلافی معنادار است یا نه؟ چطور متوجه شویم که عدد 4 بدست آماده در این آزمایش مبناش یک واقعیت علمی هست و در فرایند تصادفی چنین tvalueای مشاهده نمی‌شود؟

راه چاره اینه که آزمایش انجام شده را با آزمایشات تصادفی مقایسه کنیم و ببینیم که آیا در آزمایش تصادفی هم چنین نتیجه ای مشاهده می‌شود؟! به عبارتی tvalue را به pvalue تبدیل کنیم .

یعنی چی ؟ یعنی بیاییم یک تعداد زیادی آزمایش تصادفی انجام بدهیم و در هر آزمایش تصادفی میزان tvalue انها را بدست بیاوریم. و در نهایت بررسی کنیم ببینیم که چند درصد از آزمایشات تصادفی tvalue ی مساوی 4 یا بیشتر از 4 دارند. به عبارتی میخواهیم بیینم که در چند درصد از این آزمایشات تصادفی، اختلافی که ما مشاهده کرده‌ایم در آنها نیاز مشاهده شده است. یا در چند درصد از این آزمایشات اختلاف بیشتری از مقدار مشاهده شده در مسئله اصلی وجود داشته است.

برای انجام این آزمایش تصادفی دو مجموعه داده تصادفی با توزیع نرمال و میانگین یکسان ایجاد میکنیم.

برای مثال A= randn(1,300) و B= randn(1,300)

با اینکه هر دو تا داده با میانگین یکسانی ایجاد شده‌اند اما از انجا که تصادفی ایجاد می‌کنیم، میانگین دو مجموعه متفاوت خواهد بود.حالا مقدار tvalue این آزمایش تصادفی را محاسبه می‌کنیم.

این آزمایش را برای مثال 1000 بار تکرار می‌کنیم. در هر تکرار دو مجموعه تصادفی با میانگین یکسان ایجاد کرده و tvalue آن را محاسبه می‌کنیم. در نهایت ما 1000 تا tvalue بدست می‌آوریم که همه آنها در فرایند یک آزمایش تصادفی ایجاد شده‌اند.

حال مقدار tvalue بدست آمده در مسئله اصلی را با این 1000 تا tvalue مقایسه می‌کنیم تا متوجه شویم که در چند تا از آزمایشات تصادفی tvalueای برابر یا بیشتر از tvalue بدست آمده در مسئله اصلی  مشاهده شده است.

برای مثال در  500 ازمایش تصادفی tvalue ها مساوی یا بیشتر از 2 است. معنییش این است که tvalue مشاهده شده در مسئله اصلی برای یکی از این 500 آزمایشات تصادفی است. تعداد خیلی زیادی است و اگر ما براساس tvalue به دست آماده بخواهیم قضاوت کنیم که ورزش کردن تاثیر مستقیمی بر روی فشار خون دارد، در آن صورت به احتمال 50 درصد اشتباه خواهیم کرد.  به این احتمال pvalue میگوییم. به عبارتی pvalue میزان احتمال خطای ما را مشخص میکند. ما یک اختلافی را مشاهده میکنیم. سپس براساس آن فضاوت میکنیم که اختلاف معنادار است. pvalue مشخص میکند که با چه احتمالی اشتباه کرده ایم.

حال اگر در این آزمایش در 50 مورد، tvalue های مشاهده شده مساوی یا بزرگتر از 4 باشند. در این صورت میتوانیم قضاوت کنیم که نتیجه کار محقق مبنای علمی دارد یا نه؟ بله . چرا که همیشه در آمار یک میزان خطا متیوانیم داشته باشیم و در این آزمایش هم 5 درصد اشتباه کرده ایم  و خطای قابل قبول است.

آیا باید در هر مسئله‌ای 1000 تا آزمایش تصادفی انجام دهیم و ببینیم که در چند درصد این آزمایشات نتیجه ما تکرار شده است؟

خیر! قبل از ما یک سری آماردان‌ها زحمت این تست‌های آماری را کشیده اند و یک جدول مشخص کرده اند. ما بعد از بدست آوردن مقدار tvalue و مشخص کردن میزان درجه آزادی (تعداد افراد گروه اول+ تعداد افراد گروه دوم -2) در جدول قرار میدهیم و مقدار pvalue را انتخاب می‌کینم.

اگر مقدار pvalue کمتر از 0.05 یا در بعضی موارد که قید شدیدتر است، کمتر از 0.01 باشد، فرضیه H1 را می پذیریم و فرضیه NULL را رد میکنیم و فضاوت میکنیم که اختلاف معنادار است ولی اگر مقدار pvalue بیشتر از 0.05  باشد، فرضیه H0 را پذیرفته و فرضیه H1 را رد می‌کنیم.