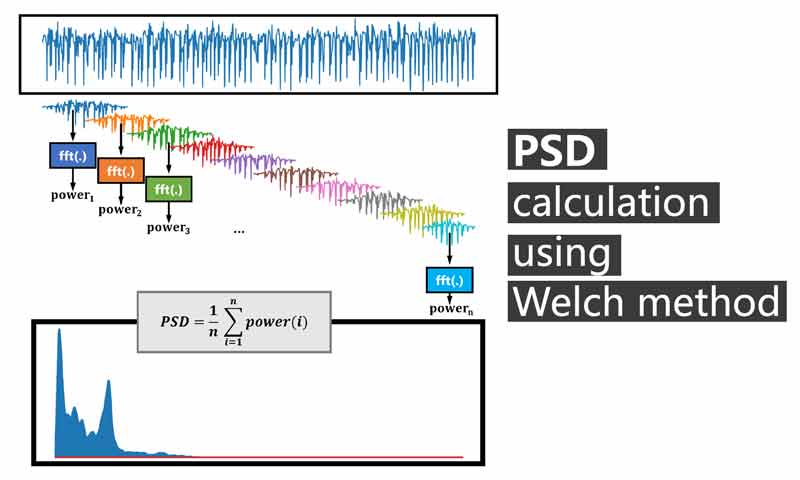
محاسبه چگالی طیفی توان PSD طبق روش welch

مفهوم چگالی طیفی توان (Power spectral density)

چگالی طیفی توان (PSD) یا طیف توان یک روشی برای ارائه توزیع مولفه های فرکانسی سیگنال ارائه میدهد که تفسیر آن به مراتب ساده از تفسیر ضرایب مختلط تبدیل فوریه است. PSD یک مفهوم اساسی است که در پردازش سیگنال برای اندازه گیری نحوه توزیع متوسط توان یا قدرت سیگنال در مولفه های فرکانسی مختلف استفاده می شود.

نحوه محاسبه توان در حوزه فرکانس

ابتدا با کمک تبدیل فوریه سیگنال را به حوزه فرکانس میبریم، سپس طبق رابطه زیر توان طیفی را محاسبه می‌کنیم.PSD از روی مربعات دامنه ضرایب فرکانسی محاسبه می شود.

ایراد این رویکرد: واریانس پریودوگرام زیاد است و به نویز حساس است.

محاسبه PSD با تکنیک Welch

روش ولش (Welch) که به احترام Peter D. Welch نام گذاری شده است. یک رویکردی برای تخمین چگالی طیفی است. از این روش برای تخمین قدرت سیگنال در فرکانس‌های مختلف استفاده می‌شود. روش ولش بهبودی در روش استاندارد تخمین طیف پریودوگرام است که در ازای کاهش رزولوشن فرکانس، نویز را در طیف‌های توان تخمینی کاهش می‌دهد. با توجه به نویز ناشی از داده های ناقص و محدود، کاهش نویز در روش ولش اغلب مطلوب است.

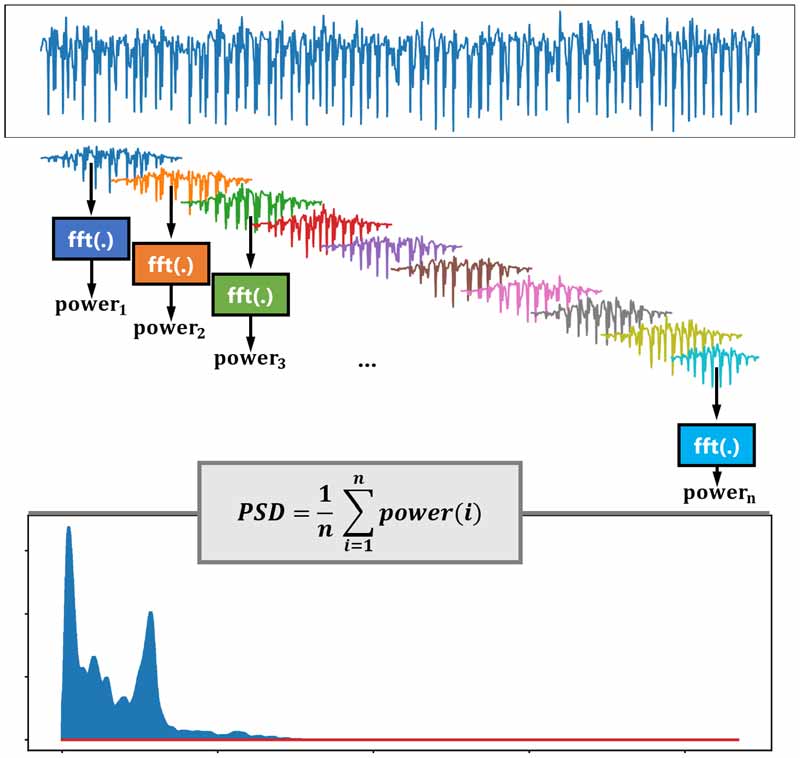
در روش Welch، با هدف کاهش واریانس پریودوگرام، به جای اینکه یکبار روی کل سیگنال تبدیل فوریه زده شود، سیگنال به چندین بازه زمانی (که معمولا باهم overlap هم دارند) تقسیم می‌شود، جهت حداقل کردن نشت طیفی (ادامه بررسی خواهیم کرد) یک پنجره روی سیگنال اعمال می شود، سپس روی هر کدام یک تبدیل فوریه زده میشود و توان هر کدام را جدا محاسبه می شود. در آخر از همه میانگین میگیرد تا چگالی طیفی توان (PSD) محاسبه شود.

پیاده سازی روش Welch برای محاسبه PSD

مرحله اول: تقسیم سیگنال به چندین بازه زمانی کوتاه

در ابتدا سیگنال به چندین بازه زمانی کوتاه تقسیم میشود. این بازه های زمانی میتوانند باهم overlap داشته باشند.

برای اینکار در ابتدا اندازه پنجره ها، میزان overlapping بین آنها را مشخص میکنیم و سپس حقله مینویسیم به تعداد بخشها، در هر تکرار یکی از بخشها را جدا میکنیم تا بتوانیم تبدیل فوریه آنرا محاسبه کنیم.

Python

nperseg= 256
noverlap= nperseg//2
nseg= sig.shape[0] // (nperseg-noverlap)
nfft= sig.shape[0]

for i in range(nseg):
    start= i*(nperseg-noverlap)
    stop= start+ nperseg
    segment= sig[start:stop]

مرحله دوم: اعمال یک پنجره (tapering) جهت حداقل کردن میزان نشت طیفی!

قبل از اینکه روی بخش جدا شده سیگنال تبدیل فوریه اعمال شود، یک پیش پردازش اولیه روی آن انجام می‌شود. جهت افزایش روزلوشن فرکانسی، یک پنجره روی سیگنال اعمال می‌شود. همانند زیر:

Python

window= np.hamming(segment.shape[0])
segment= window*segment

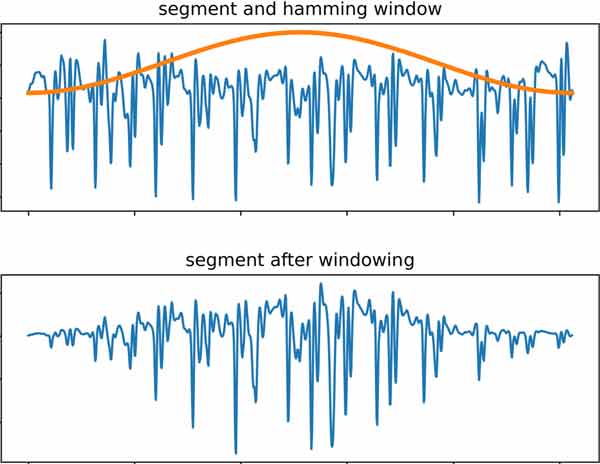
چرا windowing(tapering) انجام می شود؟

یکی از ویژگیهای تبدیل فوریه گسسته (DFT) اینه که مولفه های فرکانسی که تولید شده کاملا واضح (sharp) نیستند! در واقع، به خاطر اندازه محدودی که سیگنال ثبت شده دارد، برخی از توان که باید در یک مولفه ی فرکانسی باشد، «نشت می‌کند» به مولفه های فرکانسی کناری! این هم میتواند باعث شود که پیکهای تیز در طیف توسط چندین پیک کوچکتر احاطه شوند.

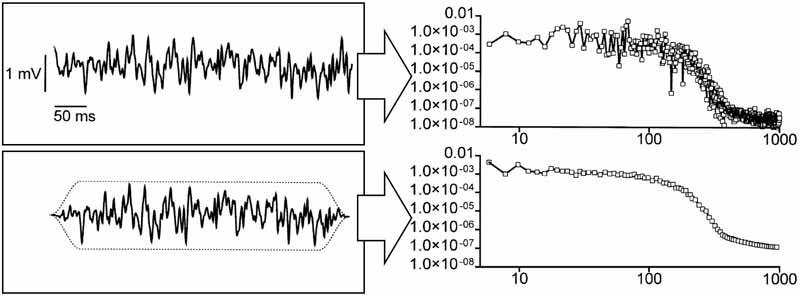
این اثر به دلیل ناپیوستگی شدید در ابتدا و انتهای سیگنال ثبت شده به وجود می آید و راه حل این است که دامنه این نمونه های کناری (اول و آخر) به آرامی به سمت صفر کاهش یابند.

با اینکار شکل هر مولفه فرکانسی تغییر میکند، به طوری که خود مولفه کمی گسترش میابد ولی مولفه های کناری به شدت کاهش می یابند و مشکل «نشت طیفی» حل میشود.

در شکل زیر اثر windowing به خوبی نشان داده شده است. روی دو سیگنال تبدیل فوریه زده شده و لگاریتم توان آنها نمایش داده شد.

مرحله سوم: اعمال تبدیل فوریه

با کمک تبدیل فوریه سیگنال از حوزه زمان به حوزه فرکانس میبریم.

نکته: برای اینکه بتوانیم در آخر از توان طیفی همه سگمنتها میانگین بگیریم، باید همگی تعداد مولفه های فرکانسی یکسانی داشته باشند. برای همین، در ابتدا مشخص میکنیم که تبدیل فوریه سگمنتها را به چندتا ضریب فرکانسی تجزیه کند.

Python

fx= fftpack.fft(segment,nfft,axis=0)

مرحله چهارم: محاسبه توان

برای محاسبه توان طیفی دو طرفه (Two-sided) طبق رابطه زیر عمل میکنیم.

Python

N= fs * np.sum(window**2)
power_sepectrum= (1 / N) * (np.abs(fx) ** 2) # two-sided psd

مرحله پنجم: محاسبه PSD با میانگین گرفتن از توان همه سگمنتها

Python

psd= np.mean(power_spectrum_all_segments,axis=0)

مرحله ششم: جدا کردن نصف توان (one-sided)

از آنجا که PSD متقارن است، نصف آن برای تحلیل و استخراج ویژگی کافی هست. برای همین نصف آنرا جدا میکنیم. فقط باید به این نکته توجه کنیم، از آنجا که نصف ضرایب را جدا میکنیم، دیگر تعداد ضرایب N نیست که تقسیم بر N شود. قاعدتا باید تقسیم بر N/2 میشد. در حالی که در ابتدا تقسیم بر N شده. برای اینکه Scale درستی داشته باشیم، کافیه مقادیر (به غیر از مقدار DC) را به 2 ضرب کنیم تا این مسئله جبران شود. انگار همان ابتدا تقسیم بر N/2 کرده ایم.

Python

# calculating one-sided psd
psd= psd[:nfft//2] # one-sided psd
psd[1:]= 2*psd[1:] # double all coefficients except DC
plt.stem(rf,psd,markerfmt='none')
plt.show()

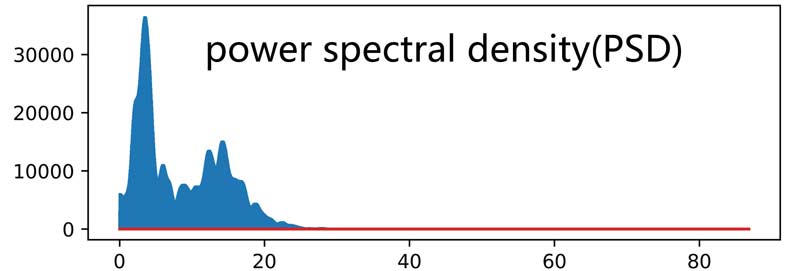
حال که PSD بدست آمده، قدم بعدی چیه؟؟؟ محاسبه توان!

محاسبه توان بازه‌های فرکانسی از روی PSD

همانطور که در ابتدا توضیح دادیم، PSD میزان توزیع قدرت سیگنال در بازه‌های فرکانسی را مشخص می‌کند. در ادامه لازم هست، که توان سیگنال به ازای بازه‌های فرکانسی مختلف محاسبه شود، تا بتوانیم از آنها به عنوان ویژگی جهت تحلیل‌های بعدی استفاده کنیم.

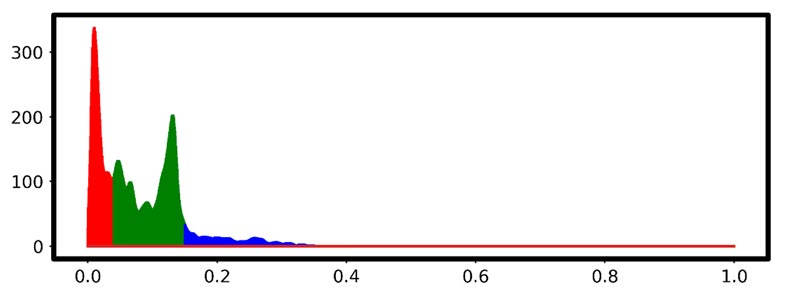
برای اینکار لازم است که سطح زیر منحنی یا به عبارتی انتگرال PSD برای بازه‌های فرکانسی (باندهای فرکانسی) را محاسبه کنیم.

الان سوال اینه که انتگرال PSD در بازه‌های فرکانسی مشخص شده رو چطوری محاسبه کنیم؟

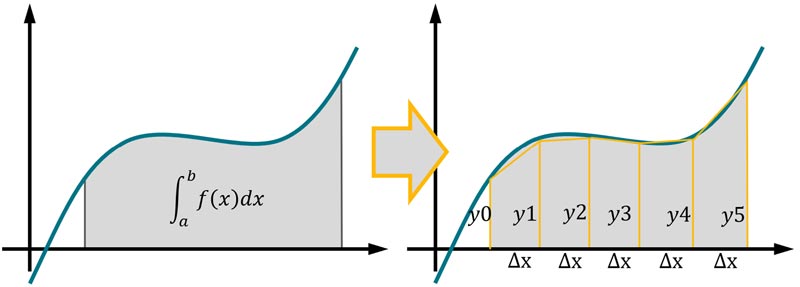
قاعده ی ذوزنقه ای (trapezoidal rule)

قاعده‌ی ذوزنقه‌ای یک روش تقریبی برای تخمین انتگرال (مساحت زیر منحنی) است. در این روش انتگرال یک منحنی با استفاده از تقسیم منحنی به تعدادی ذوزنقه کوچک محاسبه می‌شود. این یک رویکرد ساده و عملی است و برای همین خیلی در عمل استفاده می شود.

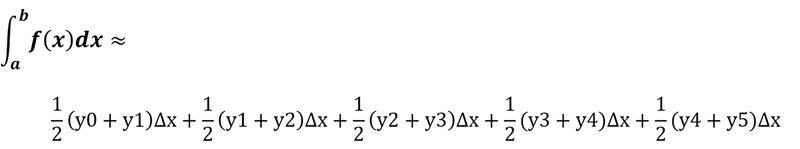
مساحت ذوزنقه

برای درک بهتر روابط بهتر است اول با یک ذوزنقه شروع کنیم. مساحت یک ذوزنقه طبق رابطه زیر محاسبه می‌شود:

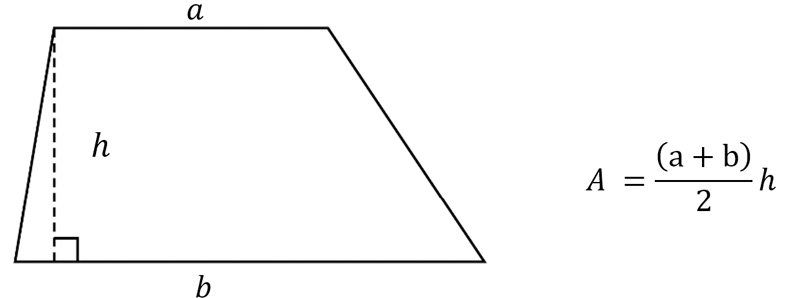
مساحت ذوزنقه قائم الزاویه

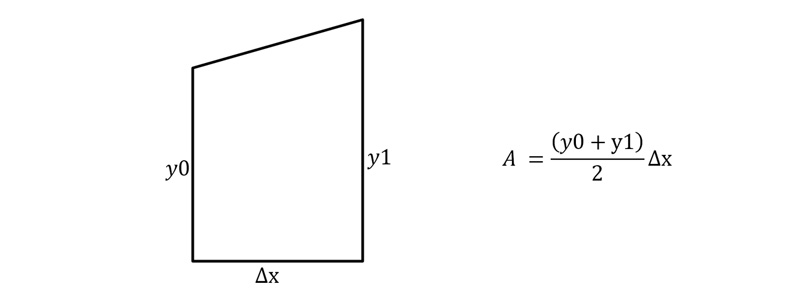
حال میتوان متوجه شد که رابطه گفته شده به چه صورت بدست آمده است. در قاعده‌ی ذوزنقه‌ای یک منحنی به تعدادی ذوزنقه کوچک تقسیم می‌شود و سپس مساحت هر ذوزنقه محاسبه شده و در آخر همه آنها باهم جمع می‌شوند تا سطح کل زیر منحنی  (انتگرال) محاسبه شود.

Python

def mytrapz(psd,f):
integral= 0
df= f[2]-f[1]
for i in range(len(f)-1):
    y1= psd[i+1]
    y0= psd[i]
    tp= 0.5*(y0+y1)*df
    integral= integral+tp

return integral

indx= np.logical_and(f>0.15,f<=0.4)
A= mytrapz(psd1[indx],f[indx])

کار تمام شد!

موفق باشید…

در «دوره پردازش سیگنال ECG» روشهای پردازش سیگنال قلبی به صورت پروژه محور آموزش داده می‌شود. یکی از الگوریتمهایی که در فصل سوم دوره آموزش داده میشود، الگوریتم Welch هست که صفر تا صد پیاده سازی شده و روی داده های مختلف اعمال می‌شود.