مطالعه مروری روش‌های بهینه‌سازی مبتنی بر گرادیان نزولی

محتوای این مطالعه مروری، خلاصه‌ای از فصل ششم دوره تخصصی پیاده‌سازی شبکه‌های عصبی با PyTorch بوده است. سعی میکنم از تصاویر بصری برای درک بهتر مطالب استفاده کنم.

دانلود فایل PDF

مباحثی که در این پست بررسی می‌کنیم:

• یادگیری در شبکه عصبی
• تابع هزینه و نقش آن در یادگیری
• فلسفه گرادیان نزولی
• محدودیت‌های گرادیان نزولی
• نرخ یادگیری متغیر با زمان
• گرادیان نزولی با ترم ممنتوم
• روش بهینه‌سازی AdaGrad
• روش بهینه‌سازی RMSprop
• روش بهینه‌سازی AdaDelta
• روش بهینه‌سازی Adam

شبکه عصبی چیست؟

شبکه های عصبی اساسا به روشهایی در هوش مصنوعی گفته می‌شوند که به کامپیوترها این امکان را میدهند که همانند مغز انسان مسائل رو حل کنند! 

شبکه‌های عصبی قابلیت یادگیری دارند! یعنی با کمک یک داده‌ای از مسئله، دانش حل آن مسئله را پیدا می‌کنند! حالا این دانش کجا ذخیره میشه؟ در وزنهای سیناپسی بین لایه‌های مختلف! این دانش چجوری بدست میاد؟ با کمک روشهای بهینه‌سازی!

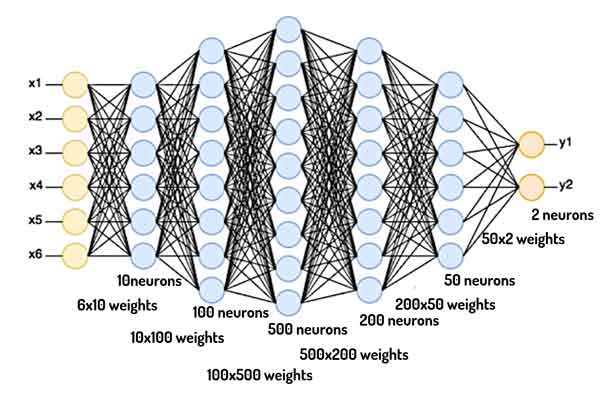
شبکه عصبی چطور یاد میگیره؟

شبکه‌های عصبی با با یک سری مقادیر اولیه تصادفی برای وزنهای سیناپسی شروع می‌کنند و در طول زمان مقادیر را بهینه می‌کنند. در هر تکرار آموزش براساس دانشی که در اون تکرار دارند یک خروجی برای داده‌های آموزش تخمین میزنند، هزینه تصمیم‌گیری شبکه توسط تابع هزینه محاسبه میشه و شبکه متوجه میشه که با خودش چند چنده و سعی میکنه اشتباهاتش رو حداقل کنه.

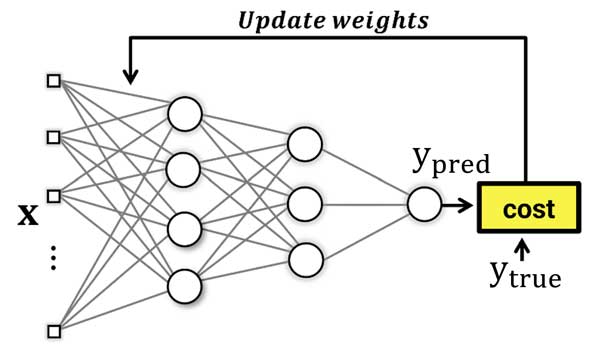
حالا مسئله اینه که شبکه عصبی چطور این خطا رو جبران میکنه! یعنی چطوری در مسیر حداقل کردن خطا حرکت میکنه!؟

تابع هزینه و پارامتر بهینه سازی

فرض کنید w پارامتر بهینه‌سازی (همان وزنهای سیناپسی شبکه عصبی) و J تابع هزینه ما هست. حالا فرض کنید که یک همچین رابطه ای بین وزنهای سیناپسی و تابع هزینه وجود دارد.

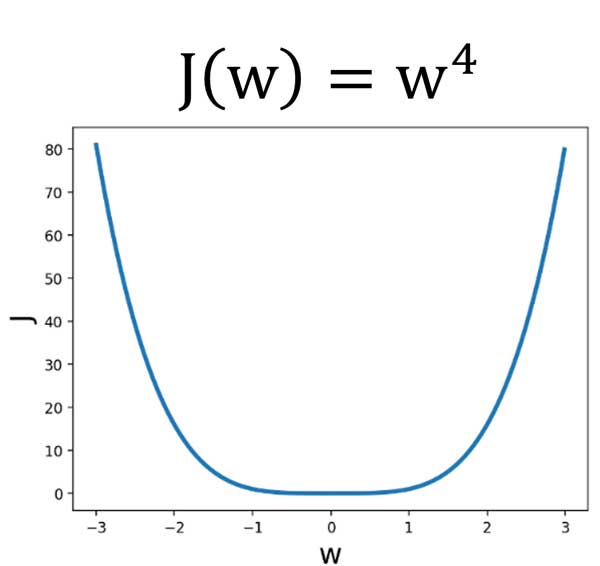
خب اگه بخواییم تصویری به مسئله نگاه کنیم، در فضای دو بعدی یک همچین رابطه‌ای بین تابع هزینه و پارامتر بهینه‌سازی وجود خواهد داشت! یعنی چی، یعنی به ازای هر مقدار w قاعدا یک میزان هزینه تصمیم‌گیری خواهیم داشت! خب گفتیم که شبکه عصبی هم با یک مقدار اولیه شروع میکنه و سعی میکنه در طول زمان وزنها رو طوری تنظیم بکنه که هزینه حداقل بشه! باید از یه جایی شروع کرد!

فرض کنید در لحظه شروع، پارامتر بهینه‌سازی ما برابر با 2.8 بوده است.

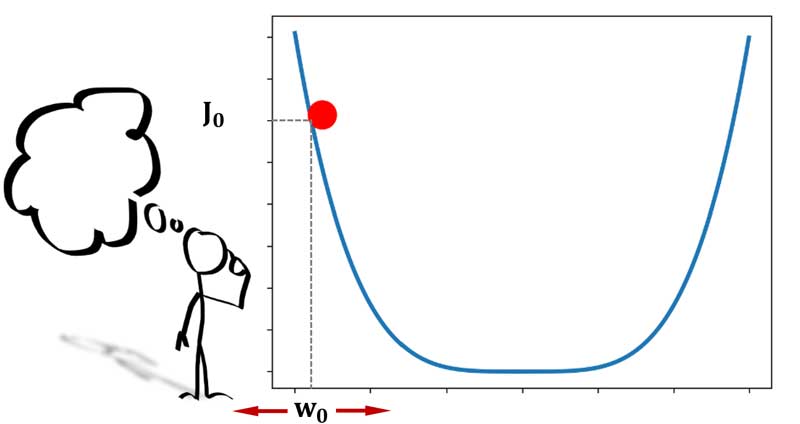
شما اگر یک روش بهینه‌‎سازی باشید و قرار باشه در طول زمان مقدار مناسب برای وزن‌های شبکه عصبی را بدست بیارید در این شکل به کدوم سمت حرکت می‌کنید تا به حداقل خطا برسید؟ چرا؟ و اینکه چطوری تشخیص میدید که کدوم سمت باید حرکت کنید؟

روشهای بهینه سازی 

چالش پایین اومدن از کوه: فرض کنید یه جای این کوه وایسادید و قراره که بیاید پایین و به سطح هموار در پایین کوه برسید. به نظرتون روشهای بهینه‌سازی چطوری این مسئله رو میبینند؟

این تقریبا شبیه چیزیه که یک روش بهینه‌سازی مسئله رو ببینه!

فرض کنید، یه جای کوه هستید و چشمان شما هم بسته است و حالا قرار که برید اون پایین پایینا! و جایی که زمین هموار شد وایسید! چطوری میرید پایین؟

خب نگاه میکنیم ببینیم کجا هستیم، بعد در جهت عکس شیب یه به عبارتی به سمت سرپایینی حرکت میکنیم تا آخرش برسیم به سمت هموار! همینکه رسیدیم سطح هموار، همونجا می‌ایستیم!

گرادیان نزولی

گرادیان نزولی هم دقیقا از همین رویکرد ما استفاده میکنه! یعنی در جهت عکس شیب خطا حرکت میکنه و زمانی که شیب خطا صفر شد وای میسه!

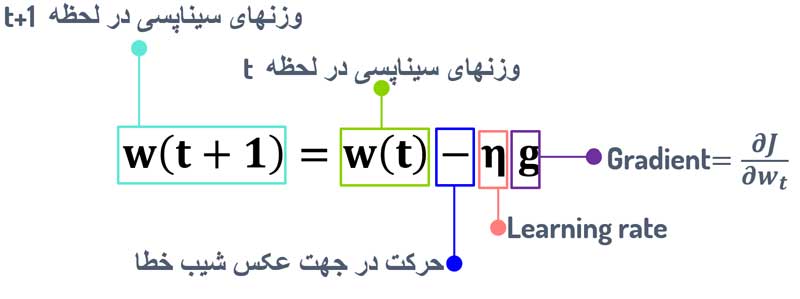
در این رابطه، w(t)  مقدار وزنهای سیناپسی در لحظه الان (t) است و w(t+1) وزنهای لحظه بعدی. η نرخ یادگیری هست که میزان تغییرات روی وزن‌های سیناپسی را کنترل می‌کند. به عبارتی گام حرکت به سمت نقطه بهینه را کنترل می‌کند! مقدار آن عددی بین (0,1) است. گرادیان نزولی به این هایپرپارامتر که توسط کاربر تعیین میشه بسیار حساس است که در ادامه بررسی می‌کنیم.

لزوم استفاده از نرخ یادگیری در گرادیان نزولی

مگه ما شیب هر لحظه رو نداریم، چرا اونو مستقیما استفاده نکنیم تا سریعتر به نقطه بهینه برسیم؟ چرا باید حتما یک پارامتری بهش ضرب کنیم که میزان تغییرات رو محدود کنه! به شکل زیر دقت کنید؟ میزان گرادیان همون ابتدا به خاطر خطای زیاد شبکه زیاد است!

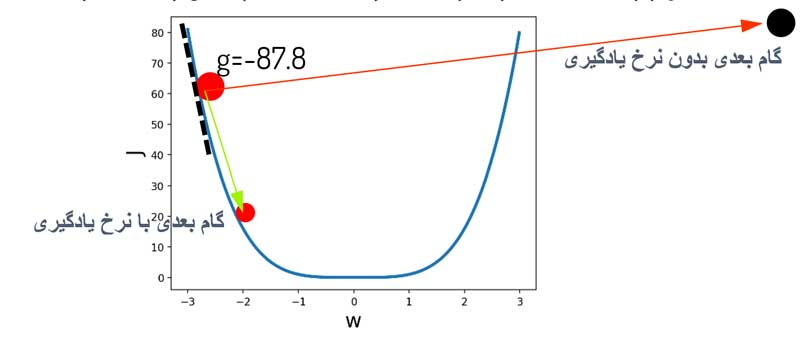
مسئله اینه که اگر از رابطه زیر استفاده کنیم و هیچ کنترلی روی تغییرات نداشته باشیم، همون اول الگوریتم از اون نقطه مینیمم اصلی هم رد میشه و ناپایدار میشه!

w(t+1)=w(t)-g=-2.8+87.8=85

ما باید یک پارامتری این وسط داشته باشیم که میزان تغییرات رو کنترل کنه تا گام به گام به سمت اون نقطه اصلی حرکت کنیم و اونو رد نکنیم. مثل این!

w(t+1)=w(t)-ηg=-2.8+(0.01*87.8)=-1.92

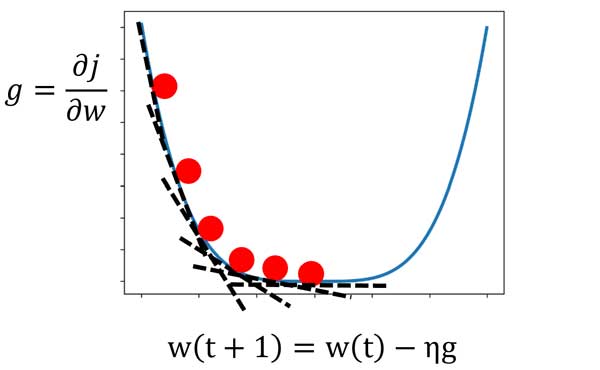
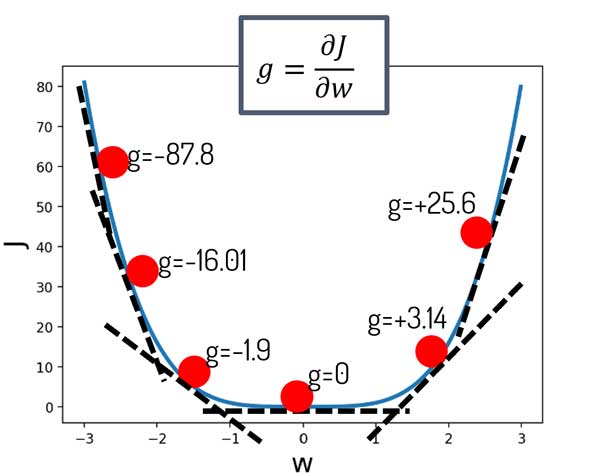
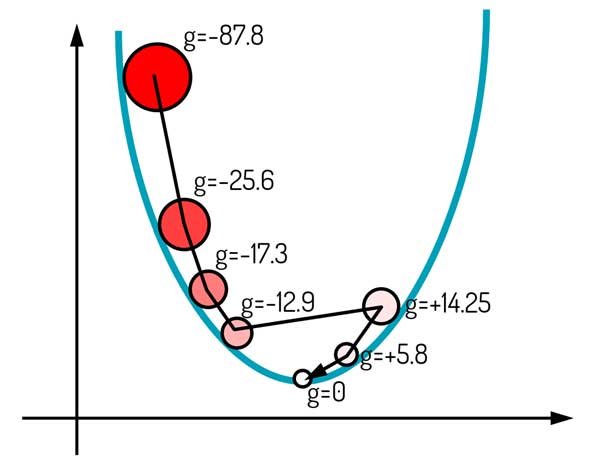
رابطه‌ی بین تابع هزینه و پارامتر بهینه‌سازی یک منحنی هست. میدونیم که شیب منحنی در هر لحظه رو میشه با مشتق محاسبه کرد. در شکل زیر مشتق تابع هزینه نسبت به پارامتر بهینه‌سازی در چندین نقطه را نشان داده ایم.

فلسفه گرادیان نزولی

گرادیان نزولی (SGD) از رابطه زیر برای تنظیم وزنهای سیناپسی شبکه عصبی استفاده می‌کند.

این رابطه معنیش اینه که گرادیان (شیب) تابع هزینه نسبت به وزنهای سیناپسیِ هر لحظه رو محاسبه کن، در جهت عکس اون شیب حرکت کن (وزنها رو تنظیم کن) تا به مقدار بهینه wای برسی که حداقل هزینه رو داشته باشد!

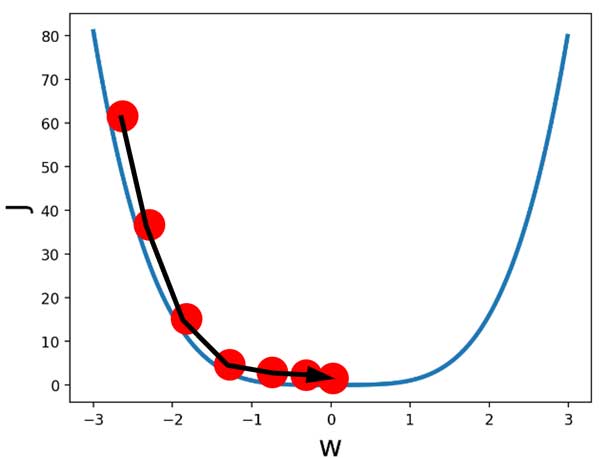
 چرا رویکرد گرادیان نزولی جواب میده؟

فرض کنید در لحظه اول w مقدار 2.8 یا -2.8 را دارد. کدوم سمت حرکت کنیم به حداقل مقدار ممکن هزینه میرسیم؟ میبینیم که در جهت عکس شیب خطا حرکت کنیم این مسئله اتفاق میافته.

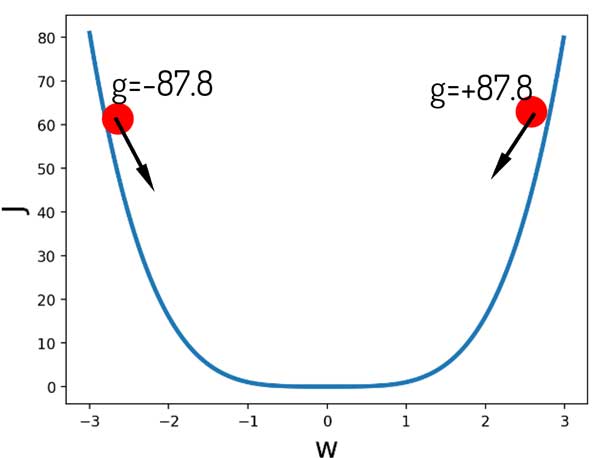
اصلا مهم نیست کدوم سمت باشیم. کافیه به گرادیان نگاه کنیم و در جهت عکس اون حرکت کنیم. بالاخره یه جایی به مقدار بهینه میرسیم!

گرادیان نزولی (SGD) از کجا میفهمه که دیگه نباید وزنها رو تغییر بده؟

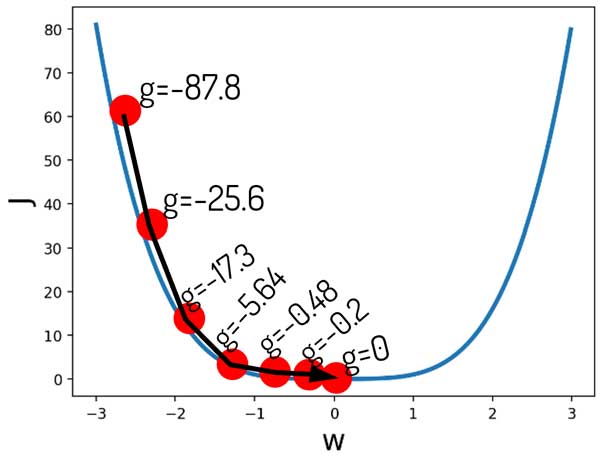
اگر دقت کنیم، بعد از چند تکرار، میزان گرادیان نزدیک به صفر میشود! و همین باعث میشه که عملا وزنهای شبکه عصبی تغییری نکنند، و به اصطلاح شبکه عصبی در مینیمم اصلی گیر بکند!

چالشهای گرادیان نزولی و مینیمم محلی

واقعیت اینه که مسائل واقعی به این سادگی هم نیستند! مثلا فرض کنید بین تابع هزینه و پارامتر بهینه‌سازی همچین رابطه‌ای وجود داره!

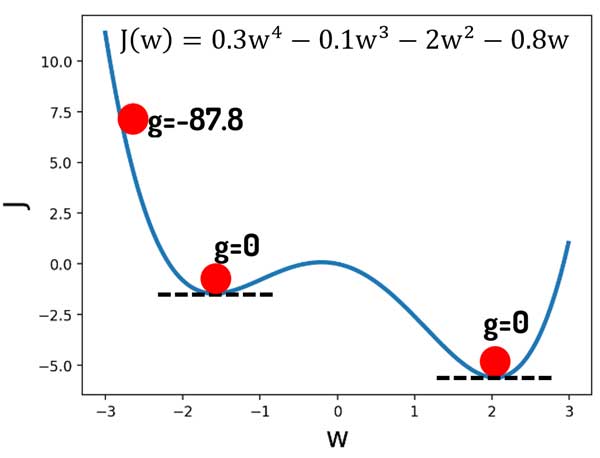
همانطور که میبینیم علاوه بر نقطه اصلی (مینیمم سراسری) یک نقطه شبیه به این نقطه داریم که بهش مینیمم محلی میگیم! در این نقاط هم شیب خطا صفر هست! در حالی که نقطه بهینه نیستند! یک چاله هستند و مدل اونجا گیر کنه کار تمومه! به اشتباه فکر میکنه که به خطای حداقل رسیده و دیگه حرکت نمیکنه و تغییری در وزنهای سیناپسی ایجاد نمیشه!

چالشهای گرادیان نزولی، مینیمم محلی و راه چاره!

این یکی از باگ‌های اصلی گرادیان نزولی است. اگر در مسیر همگرایی نقاط مینیمم محلی باشه، مدل میتونه در اونجا گیر کنه! راه چاره چیه؟!

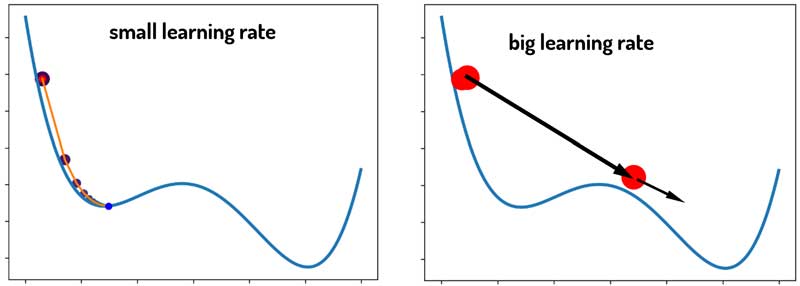
همونطور که گفتیم، گرادیان نزولی بسیار به مقدار نرخ یادگیری وابسته است و گام حرکت با کمک اون مشخص میشه. خب راه چاره چیه؟ نرخ یادگیری رو زیاد در نظر بگیریم تا گام تغییرات زیاد باشه و از نقاط محلی عبور کنیم. به همین سادگی! ایده‌ی خیلی خوبیه، نه؟!

چالشهای گرادیان نزولی  و ناپایداری

خب تعیین زیاد نرخ یادگیری هم ممکنه باعث بشه این مشکل پیش بیاد! شبکه از نقاط مینیمم محلی عبور میکنه! ولی به خاطر گام حرکت زیاد از مینیمم اصلی هم عبور میکنه! و به سمت ناپایداری میره!

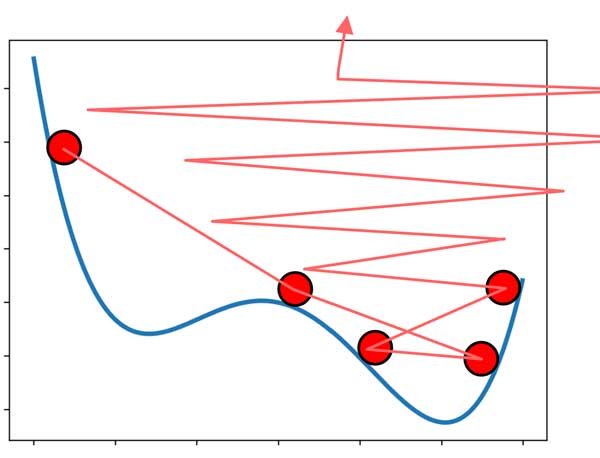
چالشهای گرادیان نزولی، مینیمم محلی و ناپایداری

به نظرتون چیکار میتونیم بکنیم تا الگوریتم نه در مینیمم محلی گیر کنه و نه به حالت ناپایداری برسه؟ مثل شکل زیر!

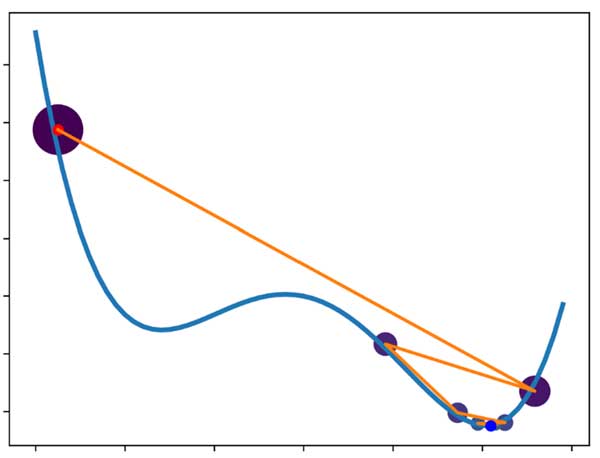
ساده ترین راه اینه که نرخ یادگیری متغیر با زمان داشته باشیم! یعنی در تکرارهای اول مقدارش زیاد باشه تا کمک کنه الگوریتم از مینیمم‌های محلی رد باشه، در تکرار‌های آخر هم کم باشه تا در مینیمم اصلی گیر بکنه و به حالت ناپایداری نرسه!

گرادیان نزولی با نرخ یادگیری متغیر با زمان

میتونیم همانند زیر به دو شکل نرخ یادگیری رو متغیر با زمان تعریف کنیم.

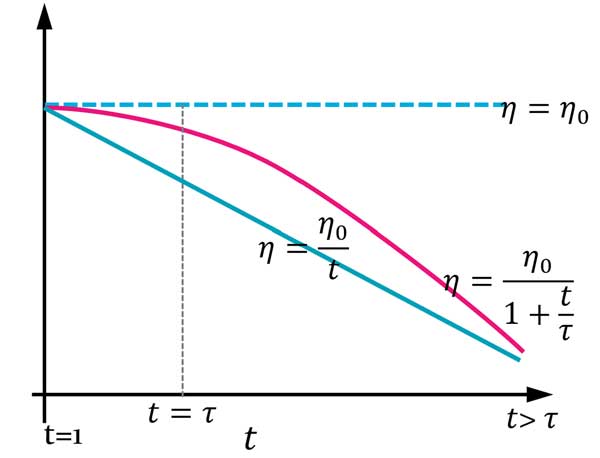
حالت اول خوبیش اینه که نرخ یادگیری متغیر با زمان است و در طول زمان به صورت خطی کم میشه! ولی ایرادش اینه که از همون اول شروع میکنه به کم کردن نرخ یادگیری! بهتر نبود اولش یه فرصتی بهش میداد، بعدش شروع به کاهش نرخ یادگیری میکرد؟ چون کاهش نرخ یادگیری از همون اول ممکنه باعث بشه الگوریتم در مینیمم‌های محلی بعدی گیر بکنه!

گرادیان نزولی: اول جستجو کن بعد همگرا شو!

روش search then converge حالت بهبود یافته شده روش قبلی است! این روش به مدل فرصت میده چند تکرار اول با گام بزرگتری حرکت کنه و بعدش از یه تکرار به بعد (t>τ) شروع به کاهش نرخ یاگیری بکنه. اینطوری سعی میکنه از نقاط مینیمم محلی اول رد بشه و در آخر هم سرعت رو کم میکنه و از حالت ناپایداری جلوگیری میکنه!

رابطه رو خودتون یبار تحلیل کنید! τ=5,η0=0.6 در نظر بگیرید و مقدار η برای 8 تکرار رو بررسی کنید.

اهمیت گرادیان لحظات قبل در گرادیان نزولی

این روشهایی که صحبت کردیم یه راهکار دم دستی هستند! باید فکر اساسی کرد!

به نظر شما گرادیان لحظات قبل چه کمکی میتونند به ما بکنند!؟ چیزی که تا الان هیچ کدام از این روشها لحاظ نکرده اند!!

گرادیان لحظات قبل در گرادیان نزولی اهیمت دارند!

ترجمه: gradients of lahazahte gabl matter

برای اینکه درک درستی از این مسئله داشته باشیم، اجازه بدید یک مثال ساده‌تری بزنیم. فرض کنید با یک ماشین در یک جاده‌ای دارید رانندگی می‌کنید. هدف چیه؟ به مقصد برسیم! دوم اینکه سریعتر به مقصد برسیم! و سوما! ماشین هم آسیب نبینه!
چجور رانندگی کنیم بهتره؟ پامون رو پدال گاز باشه و همینطوری با شتاب بریم یا نسبت به شرایط سرعت رو کم و زیاد کنیم؟ یعنی چی؟ یعنی جاهایی که مسیر هموار است به سرعتمون تا میتونیم اضافه کنیم و زمانی که به دست انداز میرسیم سریع سرعت رو بیاریم پایین که ماشین آسیب نبینه!

استفاده از گرادیان لحظات قبل در شتاب دادن به سرعت یادگیری یا کشیدن ترمز یادگیری! حالا چطور از این رویکرد در گرادیان نزولی استفاده کنیم؟

بیاید اول انتظارات خودمون از روش بهینه‌سازی رو مشخص کنیم:

• وقتی گرادیان‌ها در چند تکرار متوالی هم علامت هست سرعت رو زیاد کنیم.
• وقتی علامت گرادیان‌های چندین تکرار متوالی متفاوت است (حالت نوسانی دارد)، سرعت رو بیار پایین. چرا؟ چون الگوریتم داره به سمت ناپایداری میره و به احتمال بسیار زیاد الگوریتم در اطراف نقطه مینیمم اصلی حالت نوسانی پیدا کرده و نمیتونه همگرا بشه! سرعت رو بیار پایین تا همگرا بشه…

گرادیان نزولی با ترم ممنتوم

گرادیان نزولی با ترم ممنتوم دقیقا دنبال چنین هدفی است. میخواد از گرادیان لحظات قبل در شتاب دادن به سرعت یادگیری کمک بگیرد. ایده اش از بحث فیزیک اومده.

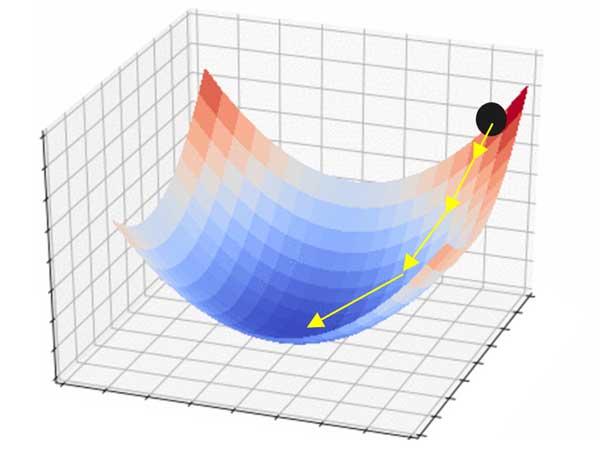
فرض کنید یک توپ (تیله) در بالای یک صفحه‌ای به شکل کاسه قرار گرفته. حالا این توپ در ابتدا با یک سرعت اولیه شروع به پایین آمدن میکنه. رفته رفته سرعت با شیب لحظه‎‌ای ترکیب شده و توپ شتاب می‌گیرد!

رابطه گرادیان نزولی با ترم ممنتوم به شکل های مختلف در کتابهای مرجع نوشته شده است که ایده‌ی همه آنها یکسان است و میخواهند گرادیان لحظات قبل رو در تنظیم پارامترهای لحظه جدید استفاده کنند.

همانطور که میبنیم، گرادیان لحظات قبل با یک ضریبی به گرادیان لحظه الان اضافه می‌شوند. الان سوال اینه که آیا اون چیزی که ما انتظارش رو داشتیم در این رابطه اتفاق میافته؟

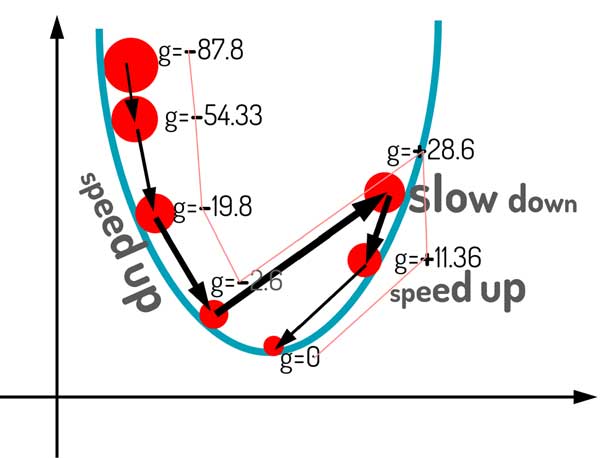
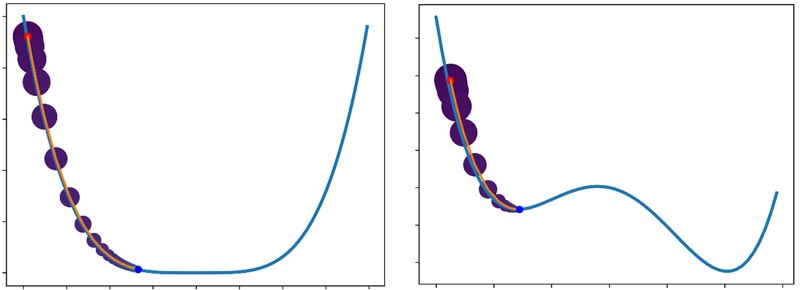
به شکل زیر توجه کنید. در اینجا از الگوریتم گرادیان نزولی با ترم ممنتوم برای بهینه‌سازی استفاده شده است. تحلیل شما چیه؟ چه اتفاقی افتاده؟

نکته: اندازه نقاط رو برحسب دامنه گرادیان نمایش دادم. 

چند تا اتفاق جالب در این مسئله بهینه‌سازی رخ داده! یکی اینکه، به خاطر استفاده از گرادیان لحظات قبل کمک کرده الگوریتم در مینمم محلی گیر نکند!
مسئله بعدی اینکه زمانی که علامت گرادیان چند تکرار متوالی یکسان بوده، سرعت رفته رفته افزایش پیدا کرده است!
سوم اینکه در انتها وقتی علامتها متفاوت بوده، سرعت کاهش پیدا کرده و الگوریتم به مینمم اصلی همگرا شده است.
بیایید ببینیم گرادیان لحظات قبل چطور کمک کردند الگوریتم در مینیمم محلی گیر نکنه.
تکرار اول| در این مسئله بهینه‌سازی مقدار اولیه w برابر -2.8 بوده است. گرادیان در لحظه اول برابر -18.29هست. چون لحظه اول هستیم فقط گرادیان اون لحظه در تنظیم پارامتر استفاده می‌شود. مقدار ترم ممنتوم 0.6 و نرخ یادگیری 0.2 در نظر گرفته شده است. با این حساب مقدار w از -2.8 به -1.33 تغییر می‌کند.

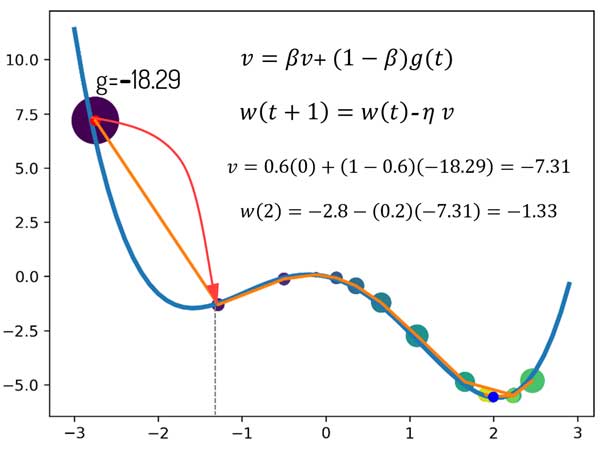
تکرار دوم| گرادیان لحظه قبل برابر با -18.29 است و گرادیان لحظه الان هم برابر با +1.145. خب با لحاظ کردن این مقادیر را در رابطه، مبینیم که مقدار w=–0.55 می‌شود. در حالی که اگر با گرادیان نزولی ساده میرفتیم جلو، w برابر با -1.55 میشد! و مدل در مینمم محلی گیری میکرد!

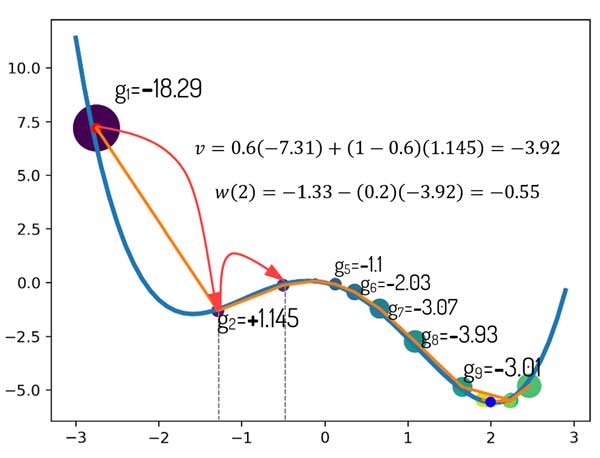
حالا اگه علامت دو تکرار متوالی یکسان بود چی میشد؟! قطعا w با یک عدد بزرگتری جمع میشد و همین باعث افزایش سرعت یادگیری میشد و الگوریتم سریعتر همگرا میشد! تکرارهای 5 تا 9 رو بررسی کنید! سرعت همینطوری رفته رفته میره بالا!

سرعت همگرایی در دو رویکرد SGD و SDG with momentum

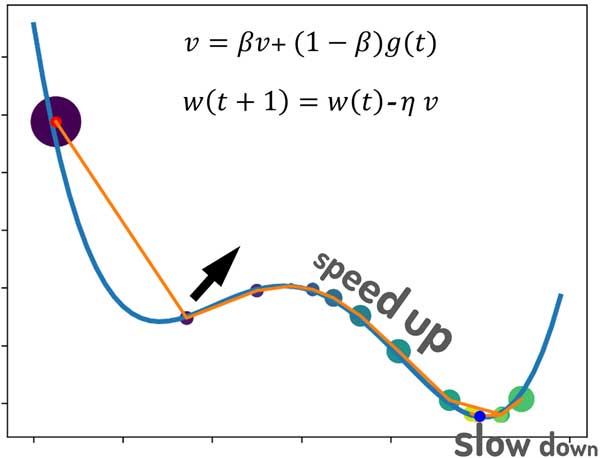
بیاید هر دو روش SGD و SGD with momentum رو در شرایط یکسان مقایسه کنیم و ببینیم که کدوم یکی از روشها سریعتر همگرا میشه. برای هر دو روش نرخ یادگیری یکسانی در نظر گرفتیم.

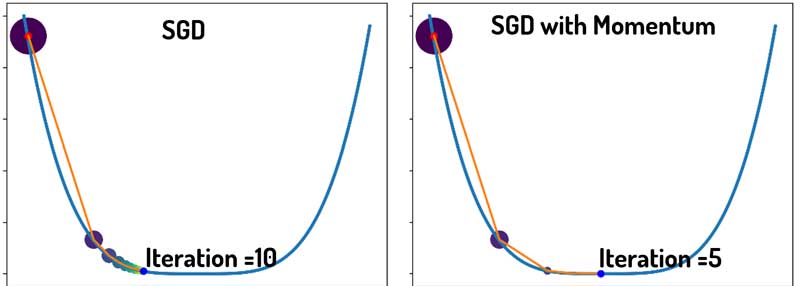
همانطور که میبیند در تکرار 5 SGD+Momentum به میینمم اصلی همگرا شده، ولی SGD در تکرار 10 هم هنوز به نقطه مینیمم نرسیده است! در این مسئله میبینیم که ترم ممنتوم کمک کرده الگوریتم سریعتر همگرا بشه!

مقدار گرادیان در لحظه رو برای هر دو رویکرد ثبت کردم و در زیر رسم کردم! چی مشاهده می‌کنید؟ قدمهای بزرگتر گرادیان نزولی با ترم ممنتوم! و همگرایی سریعتر!

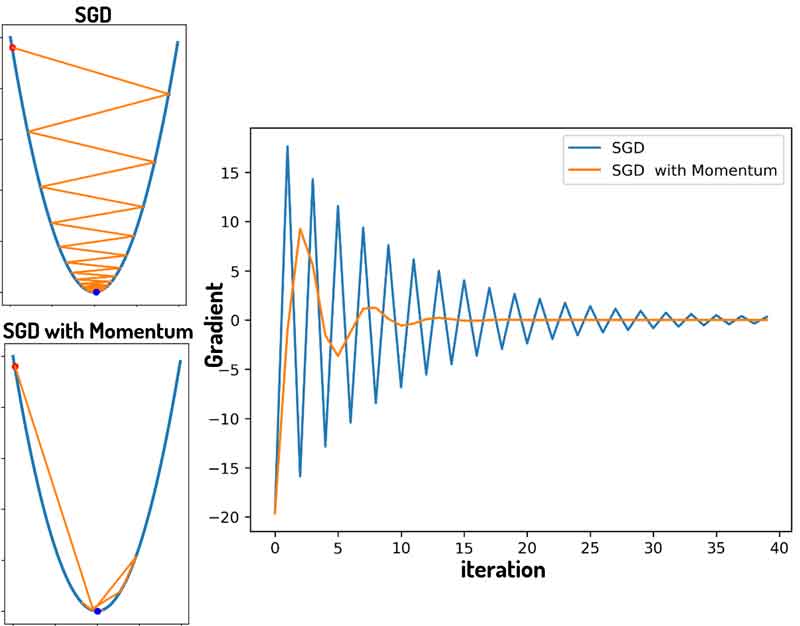
خب ممکنه بگیم، پس همه چی تمومه! هرچی لازم داشتیم این ترم ممنتوم برآورده کرده و الان خیالمون راحته که یک روش بهینه‌سازی خیلی خوب و کاملی داریم!

ولی نه، کار داریم هنوز! به نظرتون چه محدودیتی این روش میتونه داشته باشه؟ چه چیزی رو تا الان روشها لحاظ نکرده‌اند!؟

یک نرخ یادگیری و هزاران پارامتر بهینه‌سازی در گرادیان نزولی

مسئله ای که وجود داره اینه که ما در شبکه‌های عصبی، کلی وزن سیناپسی بین لایه‌ها داریم که همه آنها باید در طول زمان تنظیم شوند. و واقعیت اینه که در خیلی از مسائل، تعیین یک نرخ یادگیری مناسب برای برای همه پارامترها امکان پذیر نیست! مقدار تعیین شده قطعا برای یکی خیلی خوب و برای یکی متوسط و برای یکی خیلی بد خواهد بود و همین باعث میشه که شبکه عصبی نتونه همه وزنهای سیناپسی رو به درستی تنظیم بکنه! و دانش کافی برای حل مسئله رو بدست بیاره!

آستانه‌گذاری، یک حد آستانه‌ و هزاران پیکسل!

برای اینکه درک بهتری از این مشکل داشته باشیم اجازه بدید یک مثال ساده پردازش تصویری بزنیم. در پردازش تصویر، یک مبحثی هست به اسم آستانه‌گذاری. در آستانه‌گذاری هدف چیه؟ هدف اینه که یک تصویر سطح خاکستری رو به یک تصویر باینری تبدیل کنیم.

تصویر سطح خاکستری: تصویری هست که شامل 256 سطح روشنایی است و در آن پیکسلهای تصویر مقداری بین 0 (سیاه) تا 255 (سفید) دارند. مقدار پیکسل هرچقدر به صفر نزدیک باشه تیره تر و هر چقدر به 255 نزدیک باشه روشنتر خواهد بود.

تصویر باینری: تصویری هست که پیکسلهای آن کلا دو مقدار میتونند داشته باشند، صفر یا یک! سیاه یا سفید!

حالا فرض کنید میخواهیم یک تصویر سطح خاکستری رو به باینری تبدیل کنیم. راه ساده چیه؟ بیاییم یک سطح آستانه کلی برای همه پیکسل‌های تصویر در نظر بگیریم و پیکسل‌های تصویر را با این مقدار مقایسه کنیم، اونایی که مقدارشون بزرگتر یا مساوی حد آستانه بود به یک و اونایی که مقدارشان کمتر از حدآستانه است به صفر تبدیل کنیم.
مثلا اگر برای تصویر زیر حد آستانه 126 رو در نظر بگیریم تصویر سطح خاکستری به چنین تصویر باینری تبدیل میشه!

خب میبینیم که آستانه‌گذاری با یک حد آستانه در این مثال خیلی خوب بوده! مثل گرادیان نزولی که در بسیاری از مسائل خوب عمل میکنه!

ولی اگه background تصویر در نواحی مختلف متفاوت باشه چی؟ مثل این تصویر. آیا بازم این رویکرد میتونه جواب بده؟ قطعا نمیتونه!

میبینیم که تصویر در برخی نقاط به خوبی آستانه‌گذاری شده، ولی در برخی نقاط بسیار بد آستانه‌گذاری شده است!

راه چاره چیه؟ بیاییم برای هر پیکسل یک سطح آستانه مناسب خودش رو تعریف کنیم. در شکل زیر ما برای هر پیکسل مقدار آستانه مناسب خودش رو تعیین کردیم و به همچین نتیجه خیلی خوبی رسیده ایم!

الان دیگه باید متوجه شده باشیم که اگه بتونیم در شبکه‌های عصبی هم برای هر پارامتر، نرخ یادگیری خودش رو تعریف کنیم قطعا شبکه عصبی میتونه بهتر یاد بگیره. چرا که هر پارامتر با نرخ یادگیری مناسب خودش تنظیم میشه و به طور کلی همه پارامترها به مقدار بهینه خود همگرا می‌شوند!

روش بهینه سازی AdaGrad (adaptive gradients)

روش بهینه‌سازی AdaGrad اولین روشی بود که این ایده رو لحاظ کرد. با اینکه این روش خودش خیلی نتونست انتظارات رو برآورده کنه ولی الهام بخش توسعه روشهای خیلی بهتری شد که در ادامه بررسی خواهیم کرد.
این مقاله بالای 13 هزار سایتیش داره!

ویژگی‌های AdaGrad

تعیین سازگار نرخ یادگیری: این روش به صورت سازگار برای هر پارامتر یک نرخ یادگیری در نظر می‌گیرد و هر پارامتر متناسب با نرخ یادگیری مختص خودش در طول زمان تنظیم می‌شود!

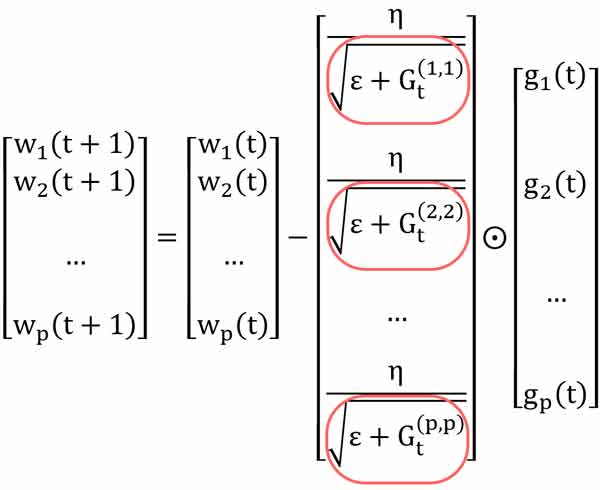
اگر به رابطه دقت کنیم، میبینیم که نرخ یادگیری کل تقسیم بر یک عدد متفاوت میشه، و از اینرو هر پارامتر با نرخ یادگیری مخصوص به خودش تنظیم میشه!

استفاده از واریانس گرادیانها: دیدیم که گرادیان لحاظ قبل بسیار اهمیت دارند و باید از آنها در تنظیم وزن‌های لحظه‌های جدید استفاده کنیم.
واریانس: واریانس غیرمتمرکز شده گرادیانها یه همچین رابطه‌ای داره.

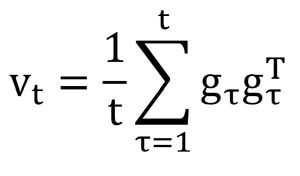
اگر به رابطه‌ی AdaGrad توجه کنیم میبینیم که رابطه Gt خیلی شبیه با وایانس هست و میشه گفت که این رابطه تقریبا همون واریانس گرادیان‌هاست.

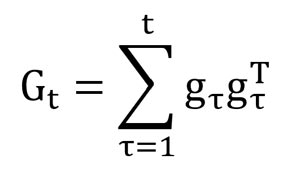
پس میشه گفت نرخ یادگیری هر پارامتر تقریبا توسط چنین رابطه‌ای مشخص میشه:

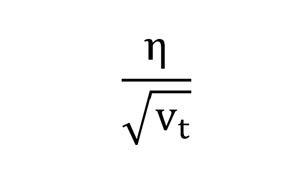
خب این چه معنی داره؟ واریانس گرادیانهای لحظات قبل چه زمانی کم و چه زمانی زیاد می‌شود؟  اگر علامت گرادیانها در چندین تکرار متوالی یکسان باشه، واریانس کم، و اگر متفاوت باشه یعنی واریانس زیاد خواهد شد!

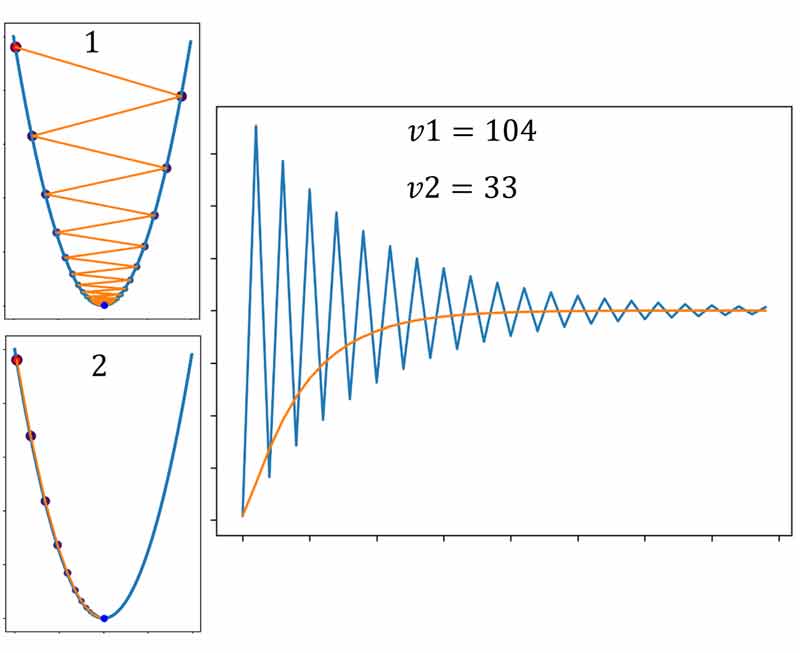
خب این چه کمکی به روند یادگیری می‌کنه!؟ مگه نگفتیم اگر گرادیان لحظات قبل علامت یکسانی داشتند باید سرعت افزایش پیدا کنه و اگه متفاوت بودند سرعت کاهش پیدا کنه؟

افزایش سرعت: به رابطه AdaGrad نگاه کنید، واریانس گرادیان‌های لحظات قبل در مخرج هست. یعنی زمانی که علامتها یکسان است واریانس کمتر خواهد بود، یعنی مخرج کم خواهد شد، پس به طور کلی سرعت یادگیری افزایش پیدا خواهد کرد!

کاهش سرعت: وقتی علامتها متفاوت باشه، واریانس زیاد خواهد بود و مخرج عدد بزرگی خواهد شد! در نتیجه نرخ یادگیری اون پارامتر کم خواهد شد و شبکه انگار ترمز میزنه و ادامه نمیده و به جای رفتن به حالت ناپایداری در مینیمم اصلی همگرا میشه!

ایراد اساسی AdaGrad

اگر دقت کنیم، روش AdaGrad هیچ کنترلی بر گرادیان لحظات قبل ندارد!

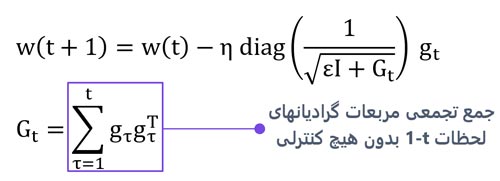
یعنی چی! یعنی همینطوری مربعات گرادیانها روی هم انباشه میشن! این باعث میشه که بعد از چندتکرار، مخرج یک عدد خیلی بزرگی بشه و نزاره وزنهای شبکه عصبی آپدیت بشند! مثل این میمونه که ترمز دستی رو کشیدید و میخواید حرکت کنید. نمیزاره اصلا ماشین حرکت کنه! ترمز دستی رو اینطور در نظر بگیرید که هر چقدر ماشین میره جلو، قدرت اصطکاکش هم افزایش پیدا میکنه! برای همین بعد از چندین تکرار دیگه ماشین نمیتونه حرکت کنه!

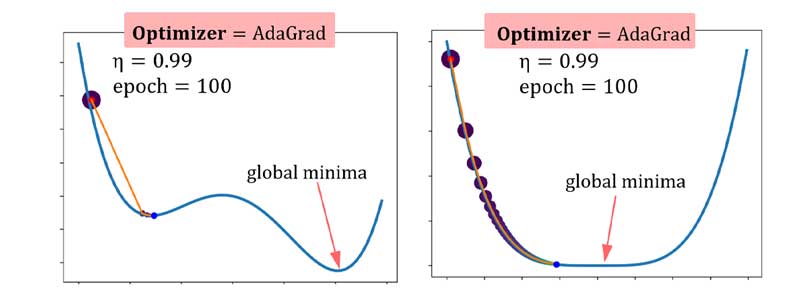
در مسائل بهینه‌سازی یعنی بعد از چندین تکرار نرخ یادگیری هر پارامتر نزدیک به صفر میشه و عملا شبکه عصبی فرصت تنظیم وزنهای سیناپسی خود رو از دست میده و نمیتونه کاری از پیش ببره! حالا اینم لحاظ کنید که اگه همون تکرار‌های اول گرادیان مقدار خیلی بزرگی باشه، دیگه اصلا امیدی به همگرایی این روش نیست! همین مسئله باعث میشه این روش بسیار وابسته به نرخ یادگیری کل η باشه، و البته در خیلی از موارد هرچقدر این رو هم بزرگ لحاظ کنیم باز هم کار به جایی نمیرسه! به مثال های زیر توجه کنید! الگوریتم اصلا نتونسته جلو بره!

روش بهینه سازی RMSprop

کنترل گرادیانهای لحظات قبل: این الگوریتم رو آقای جفری هینتون در یکی از دوره هاش مطرح کردند و مقاله ای براش نیست! رویکرد بسیار جالبی است و همین محدودیت AdaGrad رو برطرف کرده. خیلی ساده یک ترم به رابطه اضافه کرده تا تاثیر گرادیان لحظات قبل رو کنترل کنه.

γ یک هایپرپارامتر هست که مقدار آن در رنج 0 تا 1 است، و باید توسط کاربر باید تعیین شود.

حالا چرا اسمش رو گذاشتند (RMSprop)؟

RMSprop مخفف عبارت Root Mean Square propagation است و در رابطه زیر دلیلش مشخص شده است.

روش بهینه سازی AdaDelta

حذف نرخ یادگیری global: الگوریتم RMSprop  همچنان به نرخ یادگیری global وابسته است و تنظیم این میتونه در هر پروژه ای زمانبر باشه! از طرفی، اگر فرض کنیم وزنها و نرخ یادگیری آنها هر کدام یک واحد فرضی دارند و در ابتدا هم هر کدام یک مقداری هستند. در تکرار های بعدی، این واحد برای نرخ یادگیری تغییر میکنه ولی واحد وزنها بدون تغییر می مونه. این یعنی تغییرات با وزنها همخوانی ندارند! این‌ها ایراداتی هست کهAdaDelta  برای RMSprop و AdaGrad گرفته است. AdaDelta در واقع همان RMSprop هست با یک سری تغییرات.

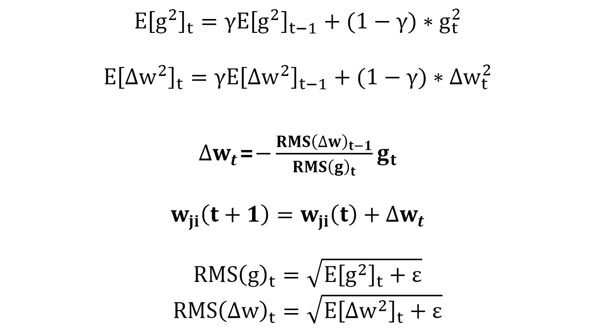
اما نتایج آزمایشات نشون میده که حذف نرخ یادگیری کل (η) خیلی هم کارساز نبوده!

روش بهینه سازی Adam

 ترکیب ممنتوم و RMSprop: الگوریتم Adam یا همان adaptive momentum term، از ویژگیهای دو الگوریتم کارآمد ممنتوم و RMSprop استفاده کرده و یک رویکرد بسیار کارامدتری ارائه داده است که در مباحث دیپ لرنینگ خیلی خوب عمل می‌کند!

hyperparameters در روش بهینه سازی Adam

سه تا hyperparameter در این الگوریتم وجود داره که باید توسط کاربر مشخص بشه! امااصلا جای نگرانی نیست. خود مقاله برای هر کدام یک مقدار پیش‎‌فرض پیشنهاد داده که اتفاقا در اکثر پروژه‌های یادگیری عمیق خوب عمل می‌کنند.

β_1=0.9, β_2=0.999,η=0.001

چرا vt و mt مستقیما در رابطه نهایی قرار نگرفته اند؟

نویسند‌گان مقاله با انجام چندین آزمایش متوجه شدند که از اونجا که mt و vt با مقدار اولیه صفر شروع می‌شوند، در همان تکرارهای اولیه این پارامترها به همون صفر بایاس میشوند و به شبکه اجازه تنظیم وزنهای سیناپسی رو نمیدهند! برای حل این مسئله، اومدند از رابطه‌ی بالا استفاده کردند. بیاید تحلیل کنیم که دقیقا اینجا چه اتفاقی میافته؟

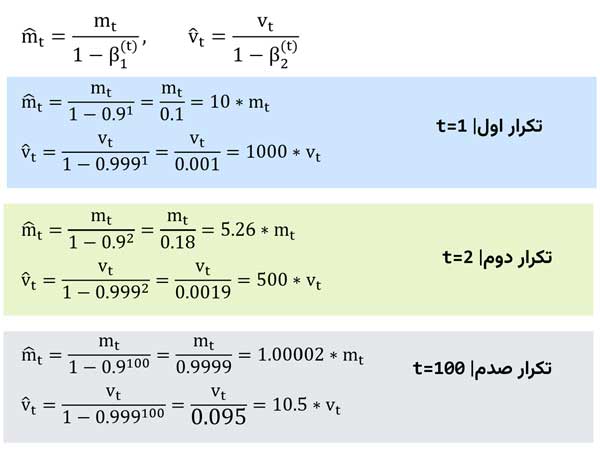
در تکرارهای اول مخرج یک عدد خیلی کمی میشه و این باعث میشه به طور کلی mt و vt چندین برابر بشند، ولی رفته رفته که تکرار بیشتر میشه، مخرج عددی نزدیک به یک میشه و تاثیری در مقادیر mt یا vt نخواهد داشت. مشکل در تکرارهای اول بود که به این سادگی حل شد!

Adam و دیگر هیچ!

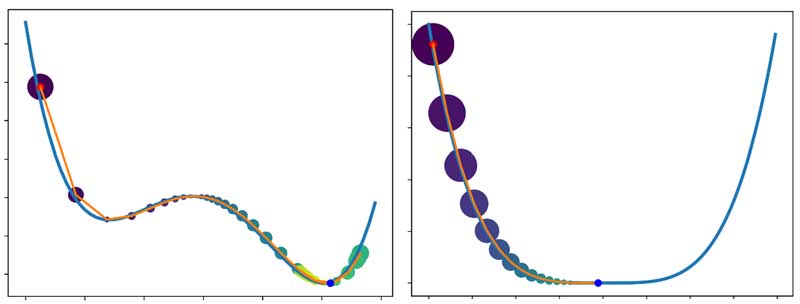
اما این پایان ماجرا نیست…

محتوای این مطالعه مروری، خلاصه‌ای از فصل ششم دوره تخصصی پیاده‌سازی شبکه‌های عصبی با PyTorch بوده است. در دوره به صورت تخصصی‌تر و با جزئیات بیشتری این الگوریتم‌ها بررسی شده و پیاده‎‌سازی می‌شوند.

علاوه بر انجام مثال‌های بسیار ساده جهت درک رویکرد و کارایی هر روش، تمامی شبکه‌های عصبی یکبار به صورت کاملا دستی و بدون ابزار آماده با کمک روش‌های بهینه‌سازی مختلف پیاده‌سازی می‌شوند و تاثیر آنها نیز در پروژه‌های عملی مختلف بررسی می‌شود.
در فصل هفتم، با ابزار PyTorch (ماژول optim, torch.nn و …) و ویژگیهایی  که دارد (autograd)، شبکه‌های عصبی را پیاده‌سازی کرده و در پروژه های عملی استفاده می‌کنیم.

دانلود فایل PDF

منابع| مباحث این دوره طبق مراجع معتبر گرداوری شده که چند تا از آنها در زیر آورده شده است.

• Deep Learning (Ian Goodfellow, Yoshua Bengio, Aaron Courville)
• Neural Networks and Learning Machines (Simon Haykin)
• Articles
  • ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
  • Adaptive Sub gradient Methods for Online Learning and Stochastic Optimization
  • An overview of gradient descent optimization algorithms