فرق بین انحراف معیار(standard deviation) و خطای استاندارد(standard error)

انحراف معیار(standard deviation)  کمیتی است که میزان پراکندگی نمونه‎های هر مجموعه حول میانگین را مشخص می‌کند. و خطای استاندارد (standard error)به لحاظ مفهومی مشخص می‌کند که این میانگین‌ها را با چه خطایی محاسبه کرده‌ایم. ما معمولا در مقالات میبینیم که نمودارهایی به شکل زیر رسم شده است.

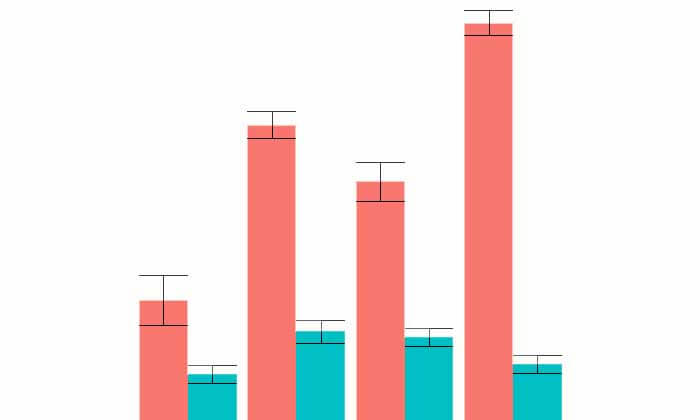
به این نمودارها اصطلاحا barplot می‌گوییم. در این نمودارهای روی هر bar یک خط کشیده شده است. به نظر شما این خطوط چه معنی دارند؟ به این خطوط  error bar یا خط خطا می‌گوییم الان سوال این است خط خطا را چطور میتوان محاسبه کرد؟ طول bar ها میانگین داده ها است و با میانگین گرفتن از sample ها میتوان محاسبه کرد.  Error bar به نوعی معرف واریانس است و به دو روش میتوان آنرا محاسبه کرد: خطای استاندار و انحراف معیار.  ولی سوال این است که چه زمانی از انحراف معیار و چه زمانی از خطای استاندارد استفاده میکنند؟ برای درک این موضوع بهتر است با یک مثال ساده شروع کنیم.

فرض کنید میخواهیم قد افراد مردم ایران را بررسی کنیم و این توانایی را داریم که که قد 80 میلیون ایرانی را اندازه گیری کنیم.

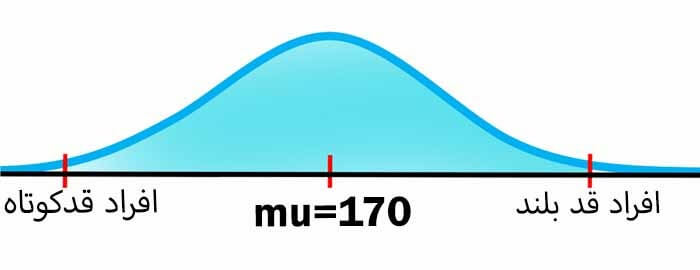
در این صورت اگر بخواهیم اگر توزیع قد افراد جامعه را رسم کنیم به همچین توزیعی خواهیم رسید. به این توزیع، توزیع نرمال می گوییم که توسط دو تا پارامتر میانگین و انحراف معیار مشخص می شود.

میانگین(mean)

میانگین نشان می‌دهد که حد وسط داده در کجا قرار دارد. در این مسئله مشخص میکند میانگین قد افراد جامعه ایران چقدر است و توسط رابطه زیر میتوان محاسبه کرد.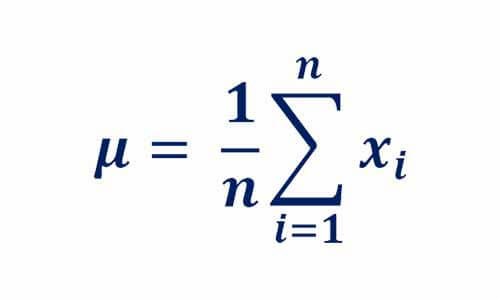

انحراف معیار (standard deviation)

انحراف میزان تغییرات یک داده حول میانگین را مشخص میکند یا به عبارت دیگر این معیار نشان میدهد که این داده چقدر پراکندگی دارد.

هر چقدر نمونه‌ها دورتر از مقدار میانگین باشند، داده‌ها پراکندگی درون کلاسی بیشتری خواهند داشت. یعنی تنوع نمونه‌ها زیاد است و  در رنج وسیعی از مقادیر توزیع شده اند و برعکس.

خطای استاندارد(standard error)

حالا فرض کنید امکان اندازه گیری قد افراد کل جامعه رو نداریم، و برای همین مجبوریم بخش کوچکی از افراد جامعه ایران انتخاب کنیم و قد انها را برای تجزیه و تحلیل اندازه گیری کنیم. فرض کنید افراد زیر از جامعه انتخاب شده اند.

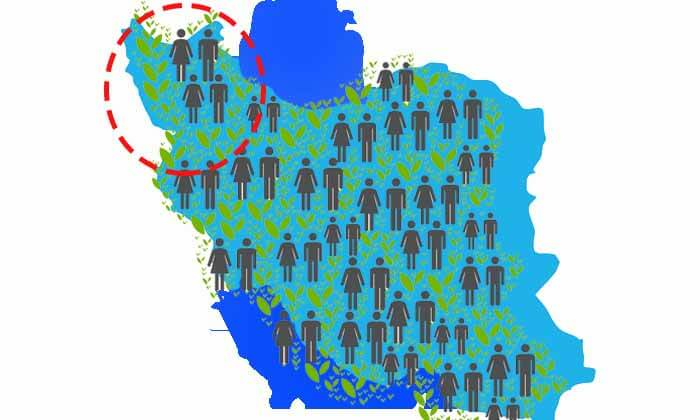
مطمئنا توزیع بدست امده برای این جمعیت محدود میانگین و انحراف معیار تقریبا متفاوتی خواهد داشت.

حال فرض کنید به جای انتخاب یک زیرمجموعه، چندین زیر مجموعه از شهرهای مختلف انتخاب کردیم. از چندین آماردان کمک گرفته ایم و از انها خواسته ایم هر کدام  یه شهری را انتخاب کرده و قد افراد اون شهر رو بررسی کنند.

هر کدام از آین آماردانها به صورت کاملا تصادفی از هر شهری یک تعداد افراد انتخاب میکنند و قد آنها را اندازه گیری می‌کنند

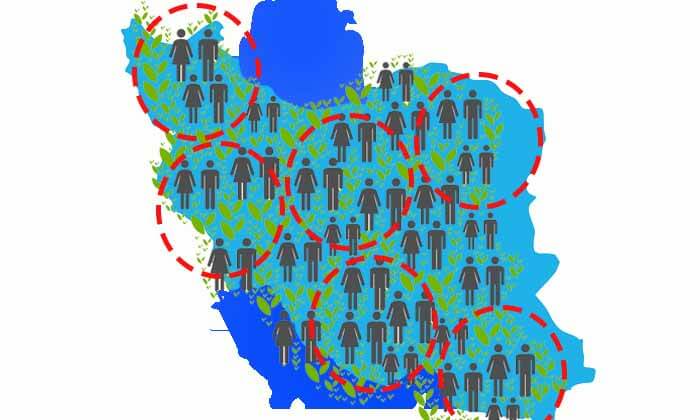
هر کدام از این آماردانها به یک توزیع تقریبا متفاوتی خواهند رسید که هر کدام میانگین متفاوتی خواهد داشت.

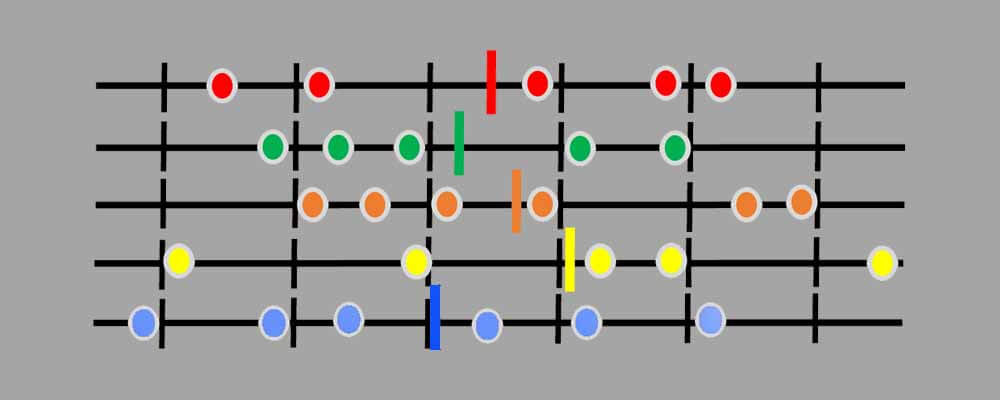
حال اگر هر کدام از این میانگین ها را یک نمونه در نظر بگیریم و توزیع آنها را رسیم کنیم مجددا به یک توزیع نرمالی میرسیم. متننها از انجا که نمونه ها میانگین ها هستند اختلاف زیادی باهم نخواهند داشت، در نتیجه توزیع نرمال بدست آماده میزان پراکندگی کمی خواهد داشت.

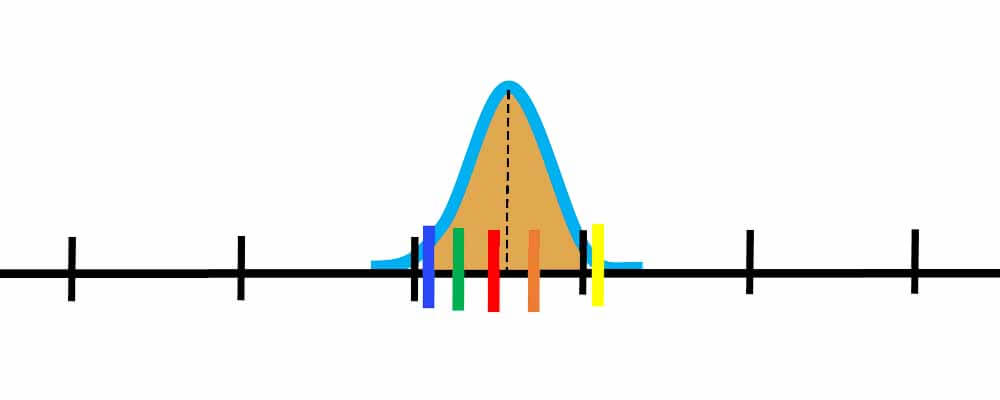
به پراگندگی میانگین ها خطای استاندارد میگوییم که  توسط رابطه زیر محاسبه می‌شود و مشخص می‌کند که میانگین‌ها با چه احتمال خطایی محاسبه شده اند!

 چه زمانی از انحراف معیار و چه زمانی از خطای استاندارد استفاده می‌کنند؟ 

مثال ماهی سالمون و سیباس را در نظر بگیرید. فعلا فرض کنید فقط ماهی های سالمون را داریم و طول همه این ماهی ها را محاسبه کرده ایم. اگر بخواهیم مشخص کنیم که تنوع طول ماهی‌های سالمون به چه صورت است از انحراف معیار استفاده می کنیم و مشخص میکند که طول ماهی های سالمون به چه صورت در بین ماهی ها توزیع شده است.

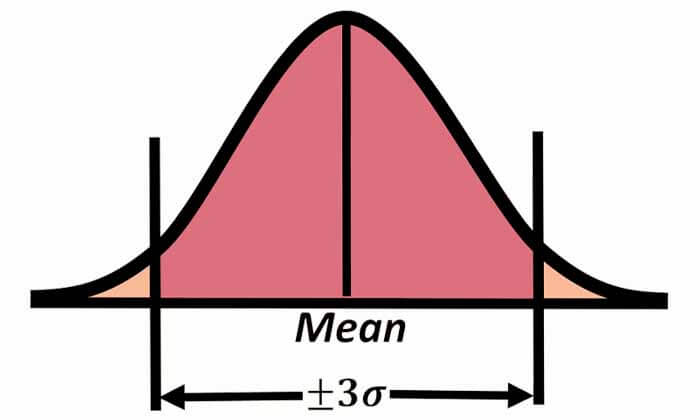
و اگر انحراف معیار را به 3 ضرب کنیم، عدد بدست آماده مشخص میکند که 99 درصد ماهی های سالمون طولشان در رنج هایلایت شده خواهد بود. یعنی اگر یک ماهی سالمون جدید انتخاب کنیم و طول آن را محاسبه کنیم، به احتمال 99 درصد طولش در رنج هایلایت شده خواهد بود.در چنین حالتهایی از انحراف معیار در نموندار barplot استفاده می‌کنیم 

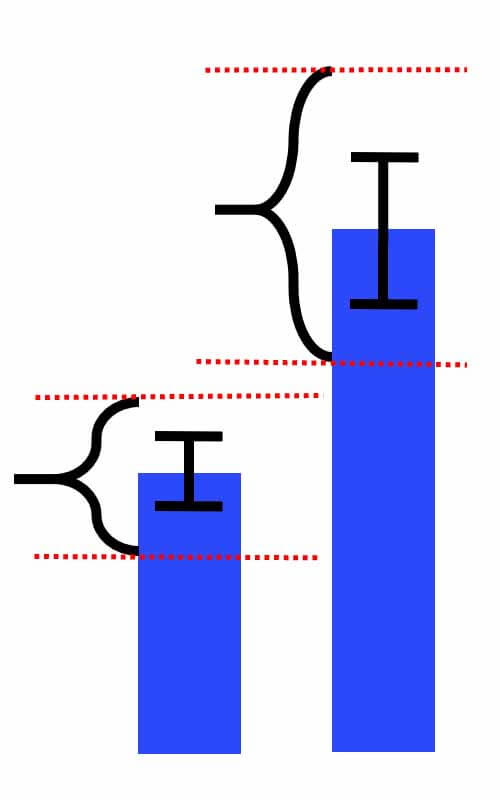
حال فرض کنید ماهی‌های هر دو گروه را داریم و طول ماهی‌های سالمون و سیباس را محاسبه کرده‌ایم. و میخواهیم کار مقایسه انجام دهیم و نشان دهیم که طول ماهی‌های سالمون و سیباس به طور معناداری باهم متفاوت هستند. در چنین حالتهایی از خطای استاندار در نموندار barplot استفاده میکنیم. اگر خطای استاندار را ضرب در 1.96 یا همان 2 بکنیم. عدد بدست آماده نشان میدهد که اگر ما دوباره این ازمایش را تکرار کنیم و دو مجموعه جدید از ماهیهای سالمون وسیباس انتخاب کنیم و طول انها را محاسبه کینم. میانگین طول ماهی های سالمون وسیباس به احتمال 95 درصد در رنج قرار خواهد گرفت اگر این رنج زیاد باشد نشان میدهد که این اختلاف معنادار نیست و طول ماهی نمی تواند ویژگی مناسبی برای تفکیک ماهیی های سالمون و سیباس باشد!