تابع هزینه cross entropy و تفاوت آن با مربعات خطا

نقش توابع هزینه در یادگیری شبکه های عصبی

در پروسه آموزش، هدف این است که شبکه عصبی وزنهای سیناپسی خود را برای حل مسئله خاصی با کمک داده آموزش تنظیم بکند. به عبارتی دانش کافی برای حل مسئله را بدست آورد. شبکه عصبی با یک مقدار اولیه برای وزنهای سیناپسی شروع میکند و در طول زمان آنها را تنظیم می‌کند.

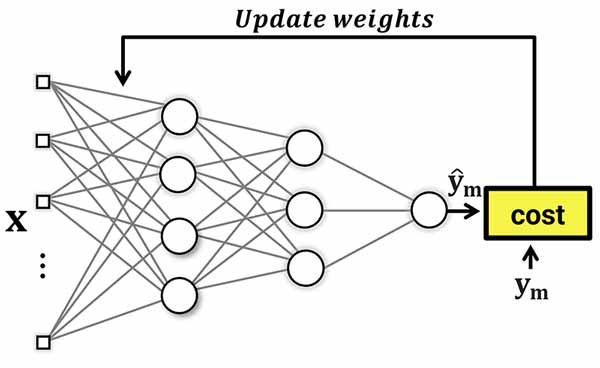
در هر تکرار آموزش، شبکه عصبی براساس مقادیر وزنهای خود (دانشی که تا آن لحظه بدست آورده است)، برای داده‌های ورودی، خروجی ای را تخمین میزند، حال برای اینکه متوجه شود که چقدر خوب یا بد عمل کرده است تا براساس آن بتواند وزنهای خود را تنظیم کند، نیاز به یک تابع هزینه دارد. توابع هزینه برای این منظور ارائه شده اند و در هر تکرار، میزان عملکرد شبکه عصبی را اندازه گیری می‌کنند و شبکه عصبی را جریمه میکنند. هر چقدر عملکرد شبکه خوب باشد، جریمه کمتر و هرچقدر عملکرد بد باشد میزان جریمه بیشتر خواهد بود.توابع هزینه با این جریمه ها شبکه عصبی را به سمت یادگیری و حداقل کردن هزینه های تصمیم گیری سوق میدهند. در یادگیری ماشین توابع هزینه ی مختلفی وجود دارد که هر کدام با هدف خاصی طراحی شده اند و خروجی تخمین زده شده شبکه عصبی را با خروجی واقعی مقایسه می‌کنند و یک هزینه ای برای شبکه عصبی محاسبه می‌کنند، سپس شبکه عصبی برای حداقل کردن این هزینه وزنهای خود را تنظیم می‌کند.

میشه گفت تابع هزینه Cross-Entropy رایجترین تابع هزینه در مسائل طبقه بندی، و میانگین مربعات خطا (MSE) رایجترین تابع هزینه در مسائل رگرسیون است. در ادامه با این توابع هزینه آشنا خواهیم شد.

حداقل مربعات خطا (mean squared error)

تابع هزینه MSE اختلاف بین خروجی تخمین زده شده‌ی شبکه عصبی و خروجی واقعی را محاسبه می‌کند و براساس مربعات این خطا (اختلاف) شبکه عصبی را جریمه می‌کند. هرچقدر اختلاف بین دو خروجی زیاد باشه، شبکه عصبی بیشتر جریمه خواهد شد و هرچقدر اختلاف بین دو خروجی کمتر باشه، شبکه عصبی کمتر جریمه خواهد شد!

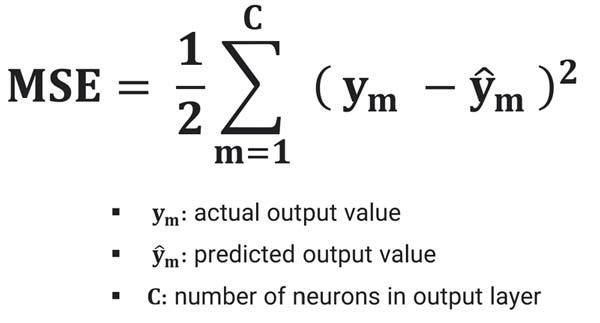
برای اینکه شبکه عصبی کمتر جریمه بشه، وزنهایش را طوری تنظیم می‌کند که حداقل خطای ممکن را داشته باشد.

تابع هزینه cross entropy

آنتروپی متقاطع یا همان Cross-Entropy میزان عدم شباهت (dissimilarity) دو توضیح احتمال را محاسبه می‌کند. در یادگیری ماشین، این تابع هزینه میزان عدم شباهت توزیع احتمال خروجی واقعی و توزیع احتمال خروجی تخمین زده شده شبکه عصبی را محاسبه می‌کند.

Cross-Entropy شبکه عصبی را به سمتی سوق میدهد که علاوه بر اینکه خروجی‌ای تولید کند که بیشترین شباهت را با خروجی واقعی داشته باشد، بلکه کلاس هدف را با سطح اطمینان بالایی نیز تشخیص دهد.

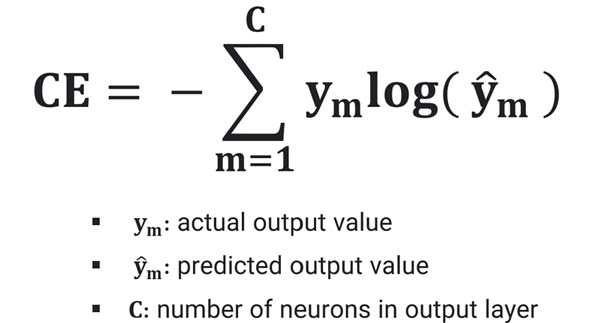
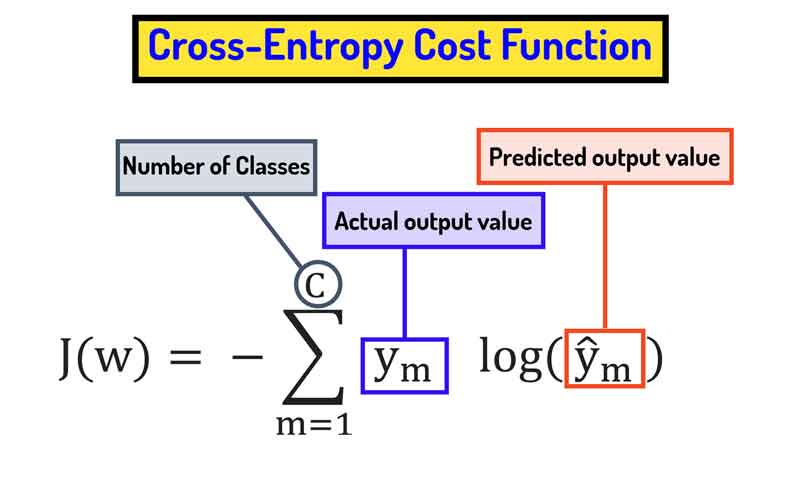
رابطه تابع هزینه cross-entropy در مسائل چندکلاسه

رابطه تابع هزینه cross-entropy در مسائل دو کلاسه

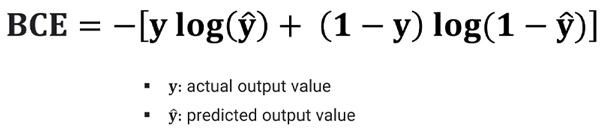
چرا تابع هزینه MSE به داده های پرت حساس است؟

توجه کنیم، که شبکه عصبی نه به ازای خطا، بلکه به ازای مربعات خطا جریمه میشه و همین باعث میشه که یه اختلاف کوچک باعث جریمه زیاد بشه، برای همین شبکه عصبی اینجا تمام تلاشش رو می‌کنه که خروجی ای تولید کنه که کمترین اختلاف را با خروجی واقعی داشته باشد. و این باعث میشه که به outlierها حساس شود. چون MSE برای داده های پرت خطای خیلی زیادی تولید میکنه و شبکه عصبی رو مجبور میکنه به اونها توجه بیشتری بکند! این یعنی داده های پرت در MSE اهمیت پیدا می‌کنند!

چرا در مسائل رگرسیون، MSE انتخاب مناسبی است؟

انتظار ما در یک مسئله رگرسیون از شبکه عصبی این است که شبکه عصبی خروجی‌ای تولید کند که کمترین اختلاف را با خروجی واقعی داشته باشد، و از آنجا که تابع هزینه MSE بر این موضوع تاکید دارد، بنابراین انتخاب خیلی خوبی میتواند برای مسائل رگرسیون باشد. ولی در مسئله طبقه بندی، فقط بحث حداقل اختلاف نیست، بلکه ما از شبکه عصبی انتظار داریم که با سطح اطمینان بالایی هم تشخیص بده. در حالی که MSE صریحا در تابع هزینه خود این موضوع رو لحاظ نکرده است.

با اینکه MSE در مسائل طبقه بندی هم عملکرد خوبی از خود نشان می‌دهد، ولی با این توضیحاتی که دادیم، نمیتواند یک انتخاب بهینه ای باشد. در ادامه با یک مثال عملی نشان خواهیم داد که چرا Cross-Entropy برای مسائل طبقه بندی انتخاب بهتری نسبت به MSE است.

چرا برای مسائل طبقه بندی cross-entropy انتخاب مناسبی است؟

انتظار ما در مسئله طبقه بندی چیه؟ انتظار ما از شبکه عصبی در مسائل طبقه بندی اینه که اولا حداقل خطای تصمیم گیری داشته باشد، دوما تصمیمات را با سطح اطمینان بالایی بگیرد. یعنی وقتی داده مربوط به کلاس یک هست، شبکه با سطح اطمینان بالایی کلاس یک تشخیص دهد!

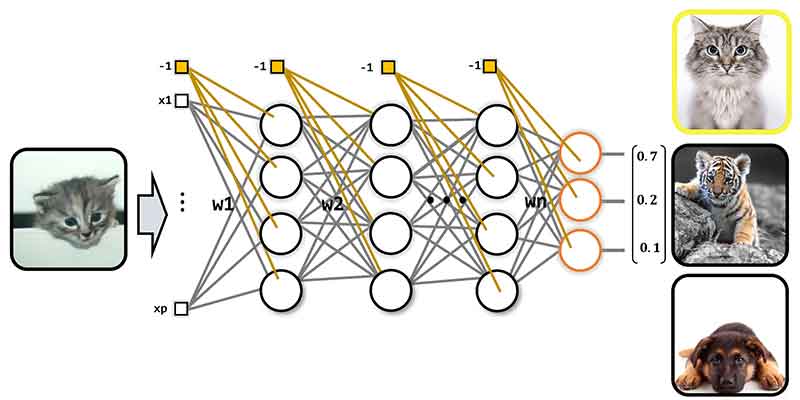
خب شبکه عصبی که خود به خود چنین چیزی رو متوجه نمیشه! باید در پروسه آموزش بهش اینو بفهمونیم. چجوری بفهمونیم؟! با جریمه و تشویق!

یعنی برای تصمیمات درستی که با سطح اطمینان بالا گرفته شده، خطای کمتری اختصاص بدهیم و برای تصمیمات درست با سطح اطمینان پایین خطای زیادی اختصاص دهیم! خب گس وات!؟ با اینکار شبکه عصبی به تصمیم گیری با سطح اطمینان بالا تشویق میشه!

از اونجا که Cross-Entropy دقیقا این دو هدف را در خود داره، برای مسائل طبقه‌بندی انتخاب خیلی خوبی است.

تفاوت cross-entropy با MSE با یک مثال عملی برای مسائل چندکلاسه؟

فرض کنید یک مسئله سه کلاسه داریم و در آن شبکه عصبی برای سه نمونه A,B و C خروجی های زیر را تخمین زده است. حال قرار هست که هزینه تصمیم گیری شبکه به ازای هر نمونه محاسبه شده و شبکه براساس آن جریمه وزنهای خود را در جهت کاهش هزینه تنظیم کنید.

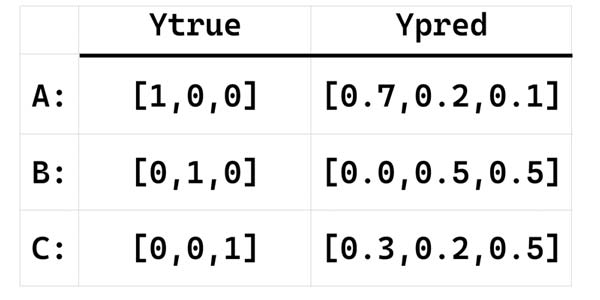
قبل از اینکه میزان جریمه توابع هزینه برای شبکه عصبی را محاسبه کنیم و بیاییم ببینیم که طبق صحبتهایی که داشتیم، هزینه ها باید به چه صورت محاسبه شوند.

خب اولا میشه گفت شبکه لیبل هر سه نمونه را درست تخمین زده ولی با سطح اطمینان پایین! پس باید شبکه به ازای هر سه نمونه جریمه بشه! بلا استثنا!

ولی از اونجا که لیبل نمونه‌ی اول را با سطح اطمینان بالاتری در مقایسه با بقیه نمونه ها تخمین زده، پس باید نسبت به بقیه جریمه کمتری داشته باشد.

و لیبل دو نمونه بعدی را با سطح اطمینان پایین و البته یکسانی تخمین زده! پس باید جریمه زیادی برای آنها محاسبه شود. از طرفی چون هر دو را با یک سطح اطمینان تصمیم گیری کرده، پس باید به یک میزان جریمه شوند! چرا؟ چون هدف ما اینه که به شبکه بفهمونیم که تخمین درست با سطح اطمینان بالا برای ما اهمیت داره، اینکه بقیه رو چی تخمین زدی مهم نیست. کلاس درست رو با سطح اطمینان بالا باید تخمین بزنی! اینطوری شبکه عصبی متوجه میشه که باید لیبلهای درست را با سطح اطمینان بالاتری تخمین بزنه!

حالا ببینیم که توابع هزینه چه جریمه ای را محاسبه می‌کنند؟

همانطور که میبینیم تابع هزینه Cross-Entropy طبق انتظاری که ما داشتیم جریمه ها را محاسبه کرده است. ولی MSE از اونجا که هدفش روی مینیمم کردن اختلاف است، برای دو نمونه دوم و سوم هزینه متفاوتی محاسبه می‌کند. به همین دلیل است که Cross-Entropy برای مسائل طبقه بندی تابع هزینه مناسبتری نسبت به MSE هست.

Python

import torch
def mse(ytrue,ypred):
    cost= torch.sum((ytrue-ypred)**2,dim=1)
    return cost

def cross_entropy(ytrue,ypred):
    cost= -torch.sum((ytrue*torch.log(ypred+1e-20)),dim=1)
    return cost  

ytrue= torch.tensor([[1,0,0],[0,1,0],[0,0,1]],dtype=torch.float32)
ypred= torch.tensor([[0.7,0.2,0.1],[0,0.5,0.5],[0.3,0.2,0.5]],dtype=torch.float32)
cost1= mse(ytrue,ypred)
cost2= cross_entropy(ytrue,ypred)
print('mse:',cost1)
print('cross entropy:',cost2)
>>> 
   mse: tensor([0.1400, 0.5000, 0.3800])
   cross entropy: tensor([0.3567, 0.6931, 0.6931])

تابع هزینه cross entropy چه پارامتری را اندازه گیری می‌کند؟

همانطور که در ابتدا اشاره کردیم، تابع هزینه cross-entropy عدم شباهت بین توزیع احتمال خروجی های تخمین زده شده شبکه عصبی و خروجی های واقعی را محاسبه می‌کند.

زمان استفاده از تابع هزینه Cross-Entropy در لایه خروجی شبکه عصبی چه تابع فعالی باید درنظر بگیریم؟

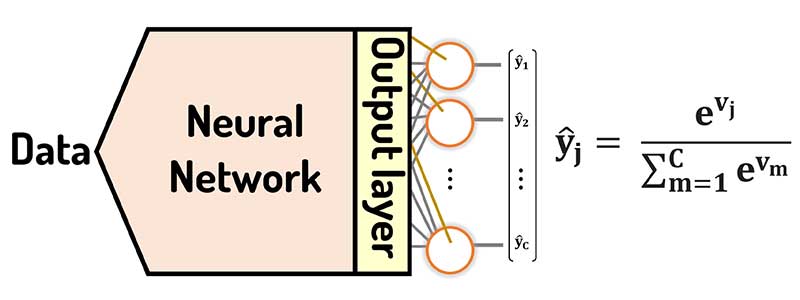
از آنجا که این تابع هزینه عدم شباهت دو توزیع احتمال را بررسی می‌کند، برای همین لازم است که خروجی تخمین زده شده، همانند یک توزیع احتمال باشد. از دو تابع فعال sigmoid و SoftMax میتوان برای این تابع هزینه استفاده کرد.

در مسائل چندکلاسه، از تابع فعال SoftMax استفاده میشود، چرا که sigmoid به ازای هر نورون یک خروجی بین صفر تا یک در نظر میگیرد و کاری با خروجی بقیه نورونها ندارد، در حالی که باید جمع همه خروجی ها یک باشد. برای همین در مسائل چندکلاسه، از تابع فعال SoftMax استفاده می‌شود.

تابع فعال SoftMax

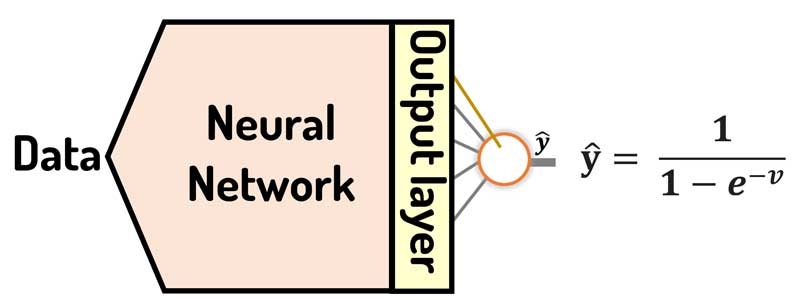
در مسائل دو کلاسه، یا به اصطلاح باینری، یک نورون در لایه خروجی استفاده میشود و برای همین از sigmoid میتوانیم همراه با تابع هزینه cross-entropy استفاده کنیم.

تابع فعال sigmoid

خروجی سیگموئید عددی بین صفر و یک هست، و میزان احتمال وقوع x به کلاس یک را مشخص میکند. یعنی اگر خروجی 0.8 باشد، معنیش اینه که احتمال نمونه ورودی به کلاس یک 80درصد و به کلاس صفر 20 درصد است.

در دوره تخصصی پایتورچ به صورت تخصصی به این مباحث می پردازیم!

ما در دوره پایتورچ سه هدف اصلی داریم:

• یادگیری تئوری و ریاضیات شبکه های عصبی و روشهای بهینه سازی
• یادگیری کار با ابزار پایتورچ به صورت تخصصی
  • ساخت dataloader ها اختصاصی برای داده های خودمان
  • پیاده‌سازی شبکه های عصبی با ابزار پایتورچ
• انجام پروژه های عملی