درک ROC و AUC

پس از اتمام کلاسبندی، یک مدل با آماره‌های مختلفی در اختیار داریم. نگاه سریعی به Accuracy می‌کنیم و در مورد آن تصمیم گیری می‌کنیم. گاهی اوقات با وجود بالا بودن مقدار accuracy از خود می‌پرسیم چرا مدل خوب کار نمی‌کند. لازم است در مورد ROC و AUC بیشتر بدانیم و اینکه چطور می‌توانیم مدل خود را به دیگری توضیح دهیم.

برخلاف بسیاری از مفاهیم دیگر در علوم داده، منابع اندکی وجود دارند که دقیقاً توضیح دهند چه اتفاقی رخ می‌دهد و بیشتر منابع تنها بر نحوه‌ی استفاده از پارامترهای ارزیابی تمرکز می‌کنند.

1-چطور دقت یا accuracy پیش بینی‌های صورت گرفته توسط الگوریتم‌های کلاسبندی را ارزیابی کنیم?

چطور دقت پیش بینی‌های صورت گرفته را ارزیابی کنیم؟ برخلاف مدل‌های رگرسیون که از MSE یا Rsq استفاده می‌کنیم، در اینجا از Confusion matrix استفاده می‎کنیم. این ماتریس برچسب‌های پیش بینی را در برابر برچسب‌های واقعی نشان می‌دهد و همچنین مشخص می‌کند که مدل چگونه گیج شده است!

اکثر کلاسبندها، احتمال اینکه هر نمونه به کلاس متفاوتی اختصاص داده شده باشد را برآورد می‌کنند. در مورد کلاسبند باینری، کلاسبندی بین دو دسته‌ی 0 و 1 انجام می‌شود. کلاسبند یک احتمال برآورد شده مثلاً 0.65 در اختیار قرار می‌دهد. سپس باید تصمیم بگیریم که این احتمال برآورد شده را به کلاس 1 یا 0 اختصاص دهیم. این فرآیند اختصاص برچسب‌های پیش بینی شده است.

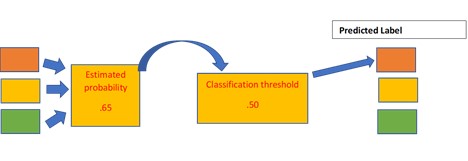
Confusion Matrix

این ماتریس برای سطح آستانه‌ی خاصی (threshold) تعریف شده است. برچسب‌های پیش بینی شده با برچسب‌های واقعی مقایسه شده و درایه‌های این ماتریس پر می‌شود.

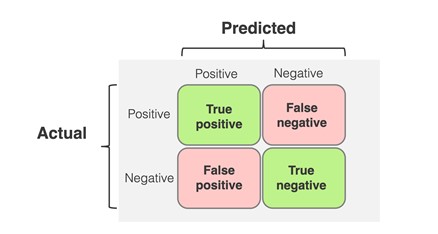
در ماتریس فوق، برچسب‌های واقعی را در سطرها و برچسب‌های پیش بینی شده را در ستون‌های ماتریس قرار داده‌ایم.

پارامترهای زیر را داریم:

True Positive (TP): اگر فرد واقعاً سرطان داشته باشد و آن را درست پیش بینی کرده باشیم.

False Negative (FN): اگر فرد واقعاً سرطان داشته باشد و او را بدون سرطان پیش بینی کرده باشیم.

False Positive (FP): اگر فرد سرطان نداشته باشد و او را سرطانی پیش بینی کرده باشیم.

True Negative (TN): اگر فرد سرطان نداشته باشد و او را بدون سرطان پیش بینی کرده باشیم.

ماتریس Confusion برای سطح احتمال آستانه‌ی خاصی تعریف می‌شود مثلاً 0.5. اگر مقدار آستانه را تغییر دهیم، ماتریس هم تغییر خواهد کرد. Confusion matrix، پایه و اساسی را تشکیل می‌دهد که از روی آن می‌توانیم معیارهای مختلفی را ایجاد کنیم و نحوه‌ی عملکرد مدل خود را سنجیده و ارزیابی کنیم.

اولین این معیارها Accuracy است:

پارامتر Accuracy اساساً نشان می‌دهد که مدل ما چقدر دقیق می‌تواند پیش بینی‌ها را به صورت درست انجام دهد. این یک معیار ساده و آسان است که در ارزیابی‌های مدل‌ها بسیار زیاد استفاده می‌شود.

چالش‌های مربوط به Accuracy

موقعیتی را درنظر بگیرید که می‌خواهیم تراکنش‌های جعلی را در مجموعه‌ی 10000 تراکنش پیش بینی کنیم.

تقسیم بندی برچسب‌ها به صورت زیر است:

غیرجعلی: 9990 و جعلی:10

تراکنش‌های جعلی، رویدادی بسیار نادر است. فرض کنید که کلاسیفایر تراکنش غیرجعلی 0 را برای تمام نمونه‌ها پیش بینی می‌کند. حتی زمانیکه accuracy برابر با 99.9% است ما نتوانسته‌ایم یک تراکنش جعلی را در دیتابیس پیش بینی کنیم.

بنابراین زمانی که دیتاس به شدت نامتقارن (imbalanced) است، معیار accuracy اگرچه معیار سرراست و راحتی برای درک است، اما ممکن است باعث سوتعبیر شود. اکثر الگوریتم‌های یادگیری ماشین که برای کلاسبندی طراحی شده‌اند فرض می‌کنند که برای هر کلاس، تعداد نمونه‌ها مشابه است.

در دنیای واقعی، دیتاست‌ها توزیع داده‌ی نامتقارنی دارند که آنها را به مسائل کلاسبندی imbalanced تبدیل می‌کند. بازنمایی اندک کلاس minority در داده‌ی آموزش باعث می‌شود که کلاسبندها در این نوع دیتاست‌ها با چالش‌هایی مواجه شوند. برای مثال در مورد مسئله پیش بینی سرطان، هزینه‌ی FN بالا خواهد بود (فردی که سرطان داشته را به عنوان فرد سالم پیش بینی کنیم) و هزینه‌ی FN از FP بالاتر است (فرد سالم را به عنوان فرد سرطانی پیش بینی کنیم).

بنابراین برای اینکه دید جامع‌تری در مورد عملکرد کلاسبند در چنین نوع دیتاست‌هایی بدست آوریم، معیارهای ارزیابی دیگری هستند که اغلب مورد استفاده قرار می‌گیرند:

1-Precision

2-Recall

معیار Precision

این معیار ارزیابی به صورت زیر تعریف می‌شود:

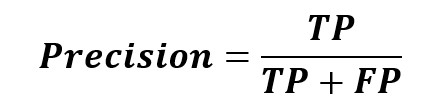
به زبان ساده، این معیار ارزیابی چنین سوالی می‌پرسد: چه تعداد از افرادی که به عنوان بیمار کلاسبندی شدند واقعاً بیمار بودند؟ زمانی از معیار Precision استفاده می‌کنیم که بتوانیم دقت پیش بینی خود را ارزیابی کنیم و اینکه چطور می‌توان از یک پیش بینی برای یک اقدام استفاده کرد.

معیار Recall

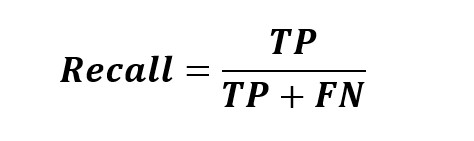
این معیار می‌پرسد که چه تعداد از بیماران واقعی توسط مدل به عنوان بیمار کلاسبندی شده‌اند. این معیار زمانی می‌تواند مفید باشد که می‌خواهیم در پیش بینی کلاس به صورت جامع‌تری عمل کنیم و زمانی که FP اهمیت کمتری نسبت به FN دارد.

2-استفاده از ROC-AUC برای ارزیابی بهتر accuracy کلاسبندی

تا به اینجا در مورد معیارهای ارزیابی که صحبت کرده‌ایم confusion matrix, accuracy, precision و recall همگی برای یک آستانه‌ی کلاسبندی خاص تعریف شده بودند. برای مثال از مقدار آستانه 0.5 استفاده کرده‌ایم یعنی نمونه‌هایی که مقدار احتمال کمتر از این مقدار آستانه داشتند در کلاس منفی و نمونه‌های با مقدار بالاتر از این مقدار در کلاس مثبت کلاسبندی شدند. این روند باعث می‌شود بتوانیم رفتار مدل را در سطوح مختلفی مشاهده کنیم. این دقیقاً همان کاری است که ROC-AUC انجام می‌دهد.

منحنی ROC

معیار Receiver Operating Curve روشی است که برای اپراتورهای رادار نظامی در سال 1941 مورد استفاده قرار گرفت و نام آن برگرفته از همین رخداد است. همچنین پس از آن به طور گسترده در تست‌های پزشکی و رادیولوژی تشخیصی استفاده می‌شده است.

معیار ROC سیستمی است که می‌خواهد تعیین کند آزمون‌های تشخیص پزشکی بین نمونه‌های مثبت و منفی چطور تفکیک قائل می‌شوند. ROC جداکننده‌ی توزیع‌های احتمال همپوشان برای نمونه‌های مثبت و منفی است. اگر همپوشانی کاملی وجود داشته باشد، سپس دو کلاس قابل جداسازی نیستند.

منحنی ROC با رسم True Positive Rate (TPR) در برابر False Positive Rate (FPR) در مقادیر آستانه‌ی مختلف رسم می‎ شود.

منحنی ROC به این صورت عمل می‌کند که TPR, FPR مدل‌ها را با هم مقایسه می‌کند. در واقع فرکانس تغییرات TP و FPها را زمانی که معیار آستانه را تغییر می‌دهیم مشخص می‌کند.

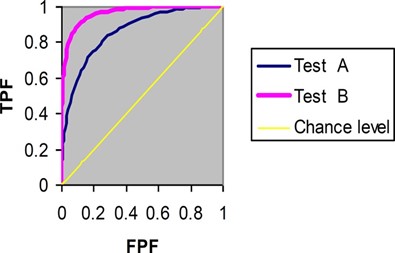
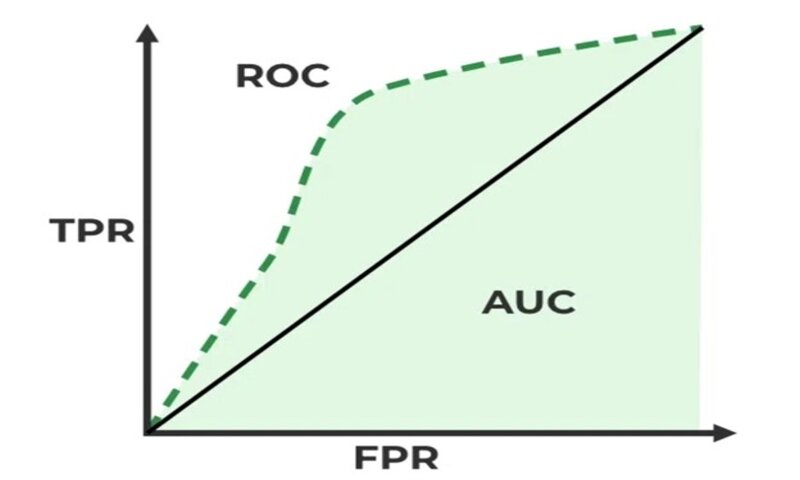
AUC که مخفف area under the ROC است. مساحت کلی آن برابر با یک است. زمانی که ROC یک خط راست است این مقدار AUC برابر با 0.5 است. این نشان می‌دهد که در هر مقدار آستانه‌ای، مدل بهتر از حالت تصادفی عمل نخواهد کرد. AUC خیلی خوب نزدیک به 1 است.

رسم منحنی ROC

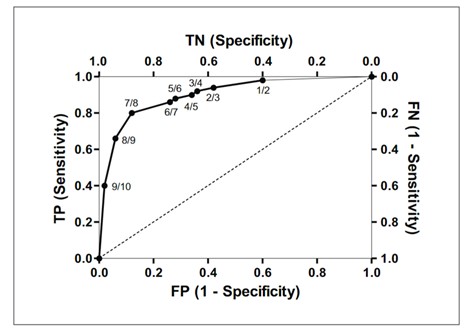
مقادیر TPR و FPR برای هر مقدار آستانه محاسبه شده‌اند و به عنوان یک منحنی ROC رسم می‌شوند.

فضای ROC  با محوری روی سمت راست و هم بخش بالا رسم شده است. مجموع نرخ TP, FN برابر با 1 است؛ زمانی که نرخ TP افزایش می‌یابد، نرخ FN کاهش می‌یابد. خط نقطه چین در شکل زیر نشانگر مدلی است که اثربخشی صفر در تشخیص نمونه‌های مثبت دارد.