تبدیل موجک چیست؟

برای درک بهتر تبدیل موجک (Wavelet Transform) ابتدا با توضیح تبدیل فوریه (Fourier Transform) آغاز می‌کنیم:

• تبدیل فوریه، اطلاعات فرکانسی یک سیگنال را در اختیار ما قرار می‌دهد و فرکانس‌های یک سیگنال و مقادیر آن را مشخص می‌کند.
• تبدیل فوریه به ما نمی‌گوید که هر فرکانس خاص در چه موقعیت زمانی در سیگنال وجود دارد، بنابراین این تبدیل برای stationary signalها بسیار مناسب است (سیگنال‌های stationary  سیگنال‌هایی هستند که با زمان تغییر نمی‌کنند و فرکانس‌های ثابت در آنها وجود دارد).
• نمی‌توانند اطلاعات فرکانسِ یک ناحیه‌ی زمانی خاص را مشخص کنند.

حال سراغ تبدیل فوریه زمان کوتاه یا Short-Time Fourier Transform (STFT) می‌رویم:

• STFT برای غلبه بر مشکل رزولوشن زمانی ضعیف تبدیل فوریه، ارائه شده است. این تبدیل یک بازنمایی Time-Frequency از سیگنال به دست می‌دهد.
• با تبدیل STFT می‌توانیم فرض کنیم که بخشی از سیگنال non-stationary، ماهیت stationary دارد.
• بنابراین می‌توانیم از هر بخش stationary در امتداد سیگنال، تبدیل فوریه بگیریم و آنها را با هم جمع کنیم.

برای مثال در شکل زیر ما یک non-stationary signal داریم، خط چین های قرمز این سیگنال را به قسمت‌های stationary تقسیم کرده اند. هر بخش مربوط به یک فرکانس خاص است و در هر بخش، فرکانس ثابت است. و در هر بخش نسبت به بخش قبل، فرکانس سیگنال افزایش می یابد.

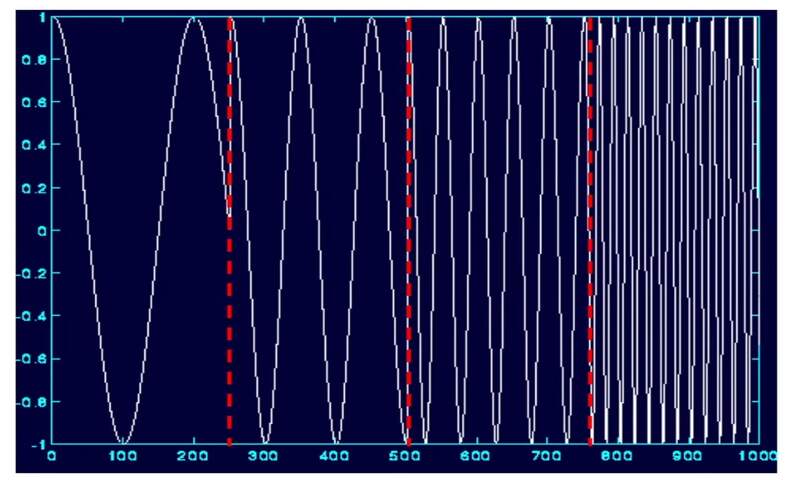
با استفاده از STFT از یک window function با طول ثابت استفاده می‌کنیم و آن را در امتداد سیگنال از آغاز تا پایان حرکت می‌دهیم و تبدیل فوریه را در هر بخش stationary بدست می‌آوریم. بنابراین window function یک مستطیل است که آن را در امتداد سیگنال عبور می دهیم.

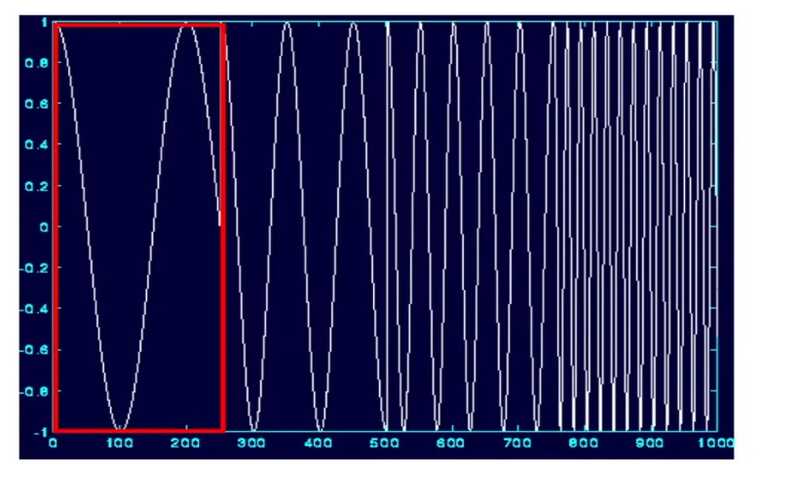
و آن را در امتداد سیگنال در هر بخش عبور می دهیم و با سیگنال در هر بخش ضرب می‌کنیم. بنابراین این پنجره روی هر بخشی که قرار می‌گیرد، مقدار دارد و در سایر بخش‌ها مقدار صفر را دارد.

رابطه ی STFT به صورت زیر است:

تنها تفاوت بین FT و STFT همین Window Function است که در STFT وجود دارد:

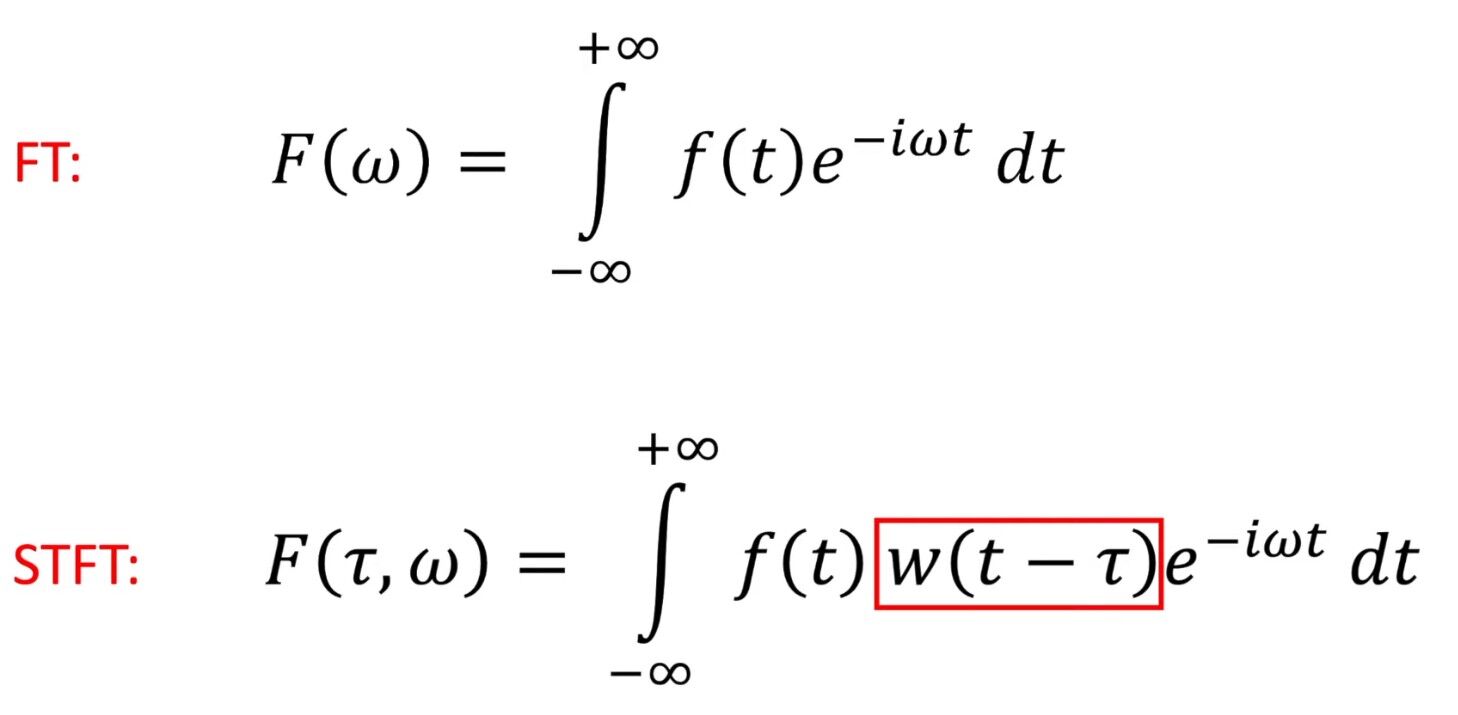
در تبدیل فوریه، تنها فرکانس داریم اما در STFT علاوه بر فرکانس، زمان هم داریم.

محدودیت‌های STFT چیست؟

• اولین محدودیت آن است که Window Function متناهی است بنابراین رزولوشن فرکانسی کاهش می‌یابد.
• دومین محدودیت آن است که طول ثابت پنجره به این معناست که رزولوشن زمانی و رزولوشن فرکانسی برای کل طول سیگنال ثابت هستند.

ما نمی‌توانیم بفهمیم در هر نمونه‌ی زمانی، چه فرکانس‌هایی وجود دارد اما می‌دانیم که چه باندهای فرکانسی در چه فواصل زمانی وجود دارند.

در شکل زیر رزولوشن زمانی و رزولوشن فرکانسی STFT به خوبی نشان داده شده است. هر چقدر پنجره ی مورد نظر باریک‌تر باشد، رزولوشن زمانی بهتر و رزولوشن فرکانسی پایین تر خواهیم داشت. هر چقدر پنجره عریض‌تر باشد، رزولوشن زمانی ضعیف تر و رزولوشن فرکانسی بهتر خواهد بود.

دو اصل بسیار مهم در رابطه با رزولوشن مکانی و زمانی:

• مولفه‌های low frequency اغلب دوره‌ی زمانی طولانی‌تری را اشغال می‌کنند. بنابراین رزولوشن high frequency  موردنیاز است.

• مولفه‌های High frequency اغلب به صورت پیک‌های کوتاه مدت ظاهر می‌شوند و بنابراین به رزولوشن زمانی بالاتر نیاز است.

تبدیل موجک (Wavelet Transform)

تبدیل موجک، سیگنال را در فرکانس‌های مختلف و رزولوشن‌های مختلف تحلیل می‌کند که Multiresolution Analysis نام دارد.

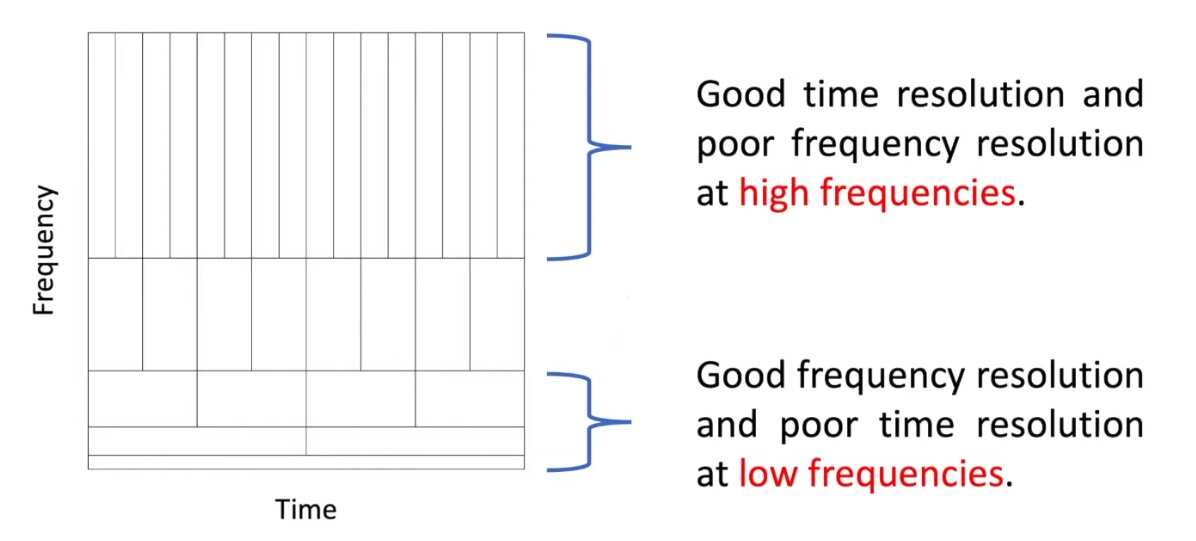
در شکل زیر عملکرد تبدیل موجک به خوبی نشان داده شده است. در فرکانس‌های بالا این تبدیل، رزولوشن زمانی خوب و رزولوشن فرکانسی ضعیفی دارد. در فرکانس‌های پایین این تبدیل، رزولوشن فرکانسی خوب و رزولوشن زمانی ضعیفی دارد.

رابطه ریاضی تبدیل موجک پیوسته به صورت زیر است که تابع ψ، تابع موجک مادر است و مفهوم رابطه این است که تابع در موجک مادر ضرب می‌شود و همچنین مقدار scale= 1/frequency ضرب می‌شود.

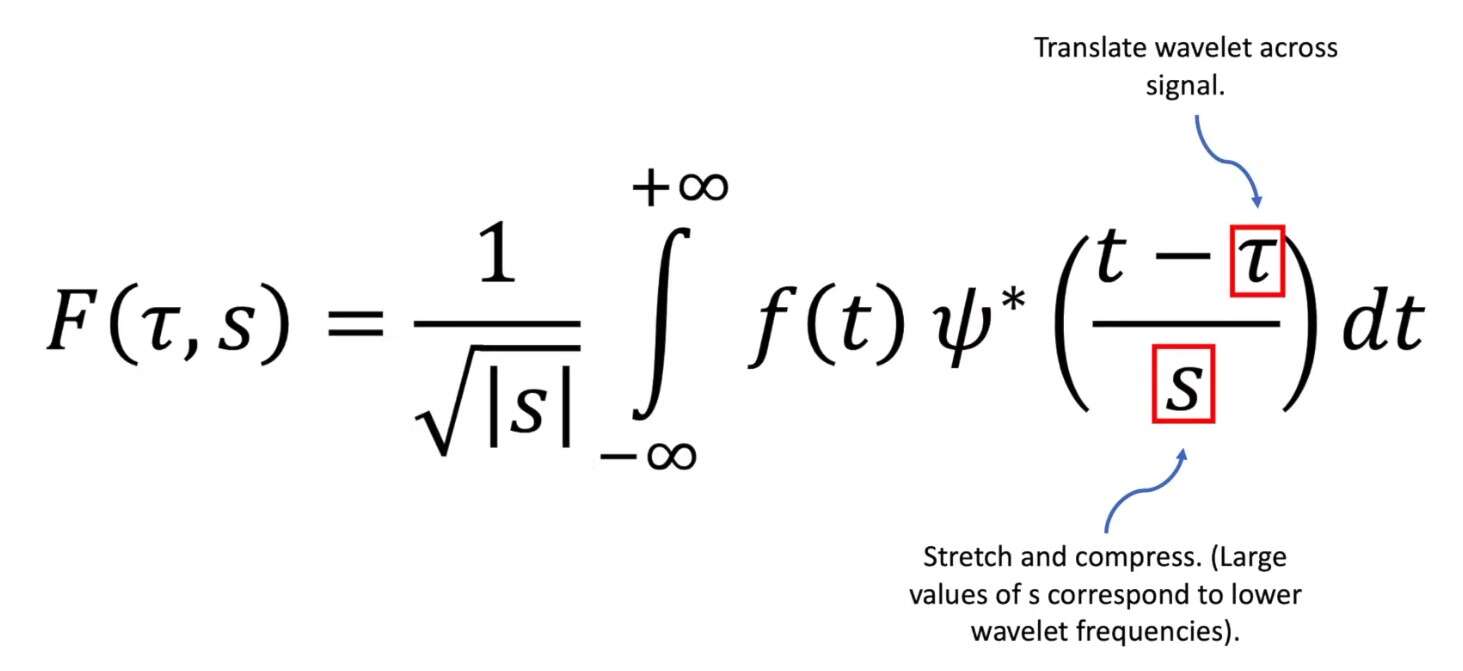
اما خود موجک مادر چیست؟

در تبدیل فوریه، توابع پایه، توابع سینوسی و کسینوسی هستند و در تبدیل فوریه ما به دنبال آن هستیم که سیگنال را با مجموعی از توابع سینوسی و کسینوسی بازسازی کنیم. در تبدیل موجک، موجک مادر، تابع پایه است و wavelet موج کوچکی شبیه به موج‌های زیر است:

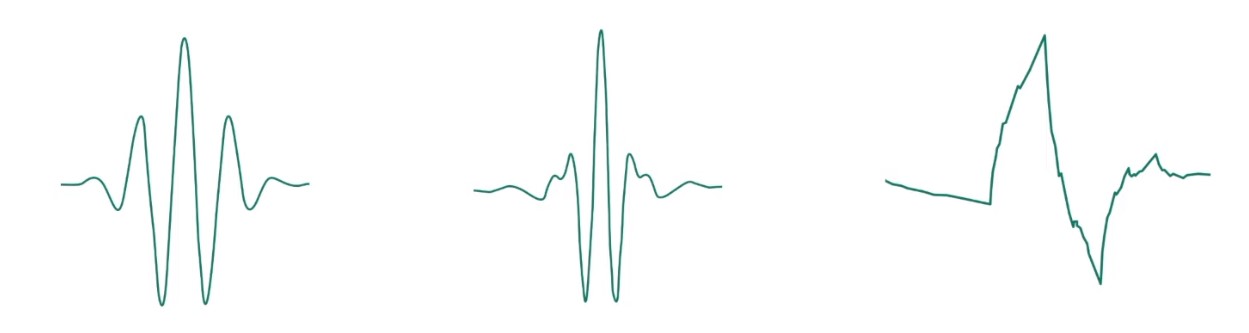
ما می‌توانیم عرض موجک و فرکانس آن را با تغییر پارامتر s، تغییر دهیم. این پارامتر s که برابر با 1 تقسیم بر مقدار frequency است، scaling نام دارد.

تمام پنجره‌هایی که در موجک استفاده می‌شوند، نسخه های فشرده شده یا شیفت یافته‌ی موجک مادر Ψ(t) هستند.

موجک‌های high-frequency، بخش‌های high-frequency سیگنال را مشخص می‌کنند و موجک‌های low-frequency بخش‌های low-frequency سیگنال را مشخص می‌کنند.

حال می‌خواهیم ببینیم تبدیل موجک گسسته (Discrete Wavelet Transform) چیست؟

• محاسبه ضرایب موجک در هر مقیاس ممکن، داده‌ی بسیار زیادی تولید می‌کند.
• اگر s, Τ  به عنوان مقادیر گسسته انتخاب شوند، آنگاه تبدیل موجک داده‌ی زیادی تولید نخواهد کرد.
• اگر s, T توان دو باشند، تحلیل بسیار موثرتر و دقیق‌تر خواهد شد

رابطه تبدیل موجک گسسته به صورت زیر است که تنها انتگرال با سیگما جایگزین شده است:

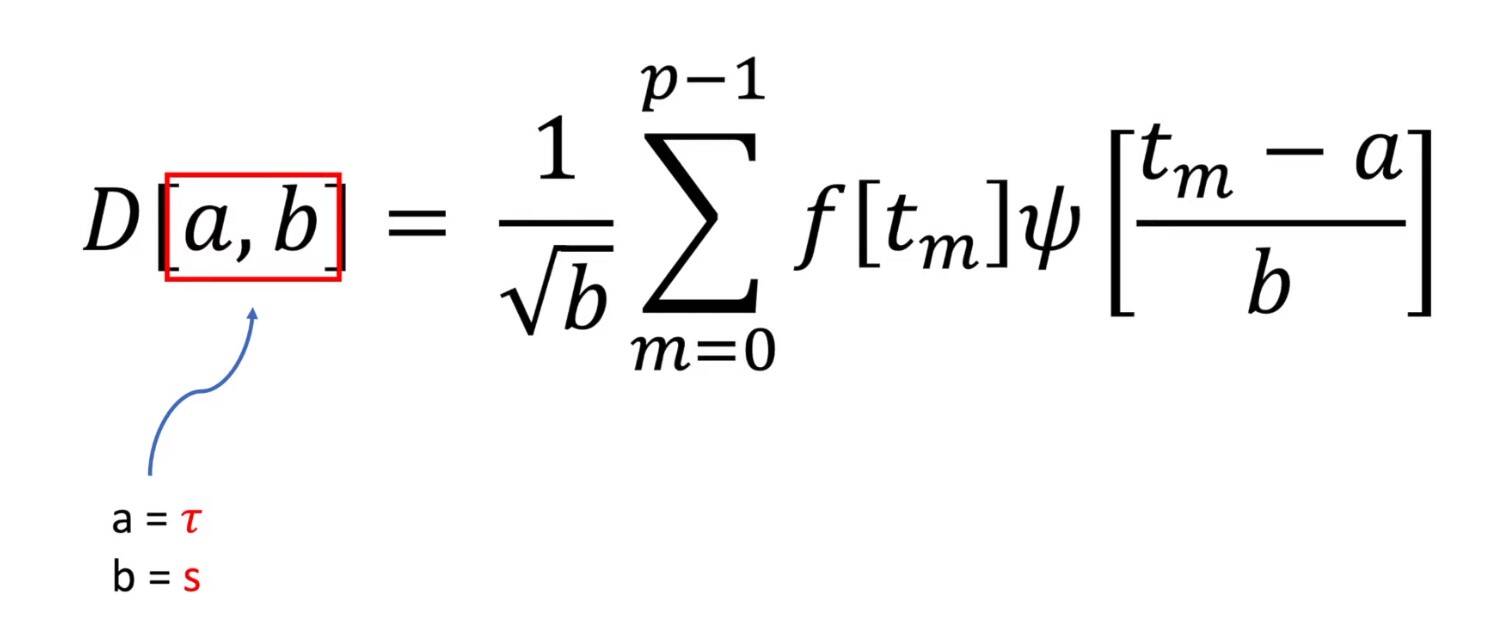
در شکل زیر نحوه ی تجزیه موجک چند سطحی با تبدیل موجک گسسته نشان داده شده است.

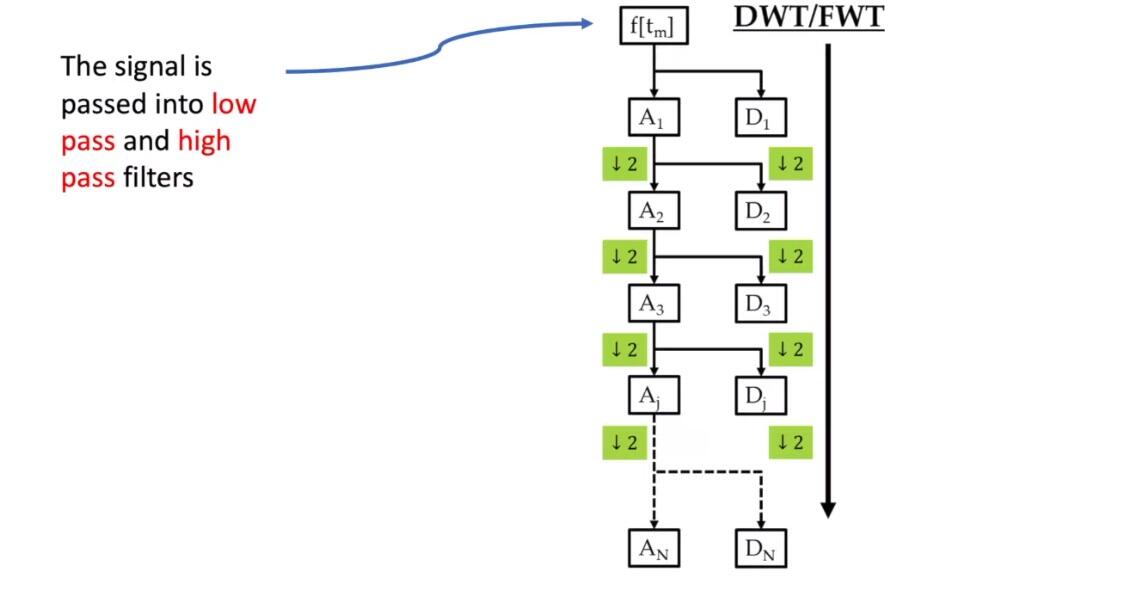
در دوره ی پردازش سیگنال مغزی با استفاده از کتابخانه MNE-Python با استفاده از تبدیل موجک از سیگنال EEG، ویژگی استخراج شده است.