مفهوم Regularization در یادگیری عمیق 

تاکنون در مورد سه تکنیک مهم در generalization صحبت شد. در این پست، به چهارمین و آخرین تکنیک از این دسته، یعنی  regularization می‌پردازیم که در کنار سه تکنیک قبل، می‌توانند همچون اکسیر، یک مدل یادگیری عمیق را کیمیا سازند.

نقش Regularization در Generalization مدلهای یادگیری عمیق

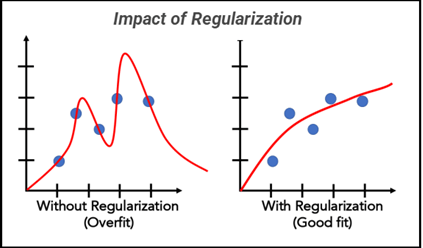
Regularization با افزودن یک جریمه به تابع هزینه مدل، که به مقدار وزن‌ها مربوط می‌شود، باعث محدود کردن پیچیدگی مدل می‌شود. به عبارتی، مدل نمی‌تواند به صورت دلخواه و بدون محدودیت، به یادگیری ویژگی‌های جزئی و نویزهای داده‌های آموزشی بپردازد. این کنترل بر روی پیچیدگی، به مدل کمک می‌کند تا مجموعه‌ای از الگوها را شناسایی کند که بیش از حد، خاص داده‌های آموزشی نیستند و در نتیجه بتواند به داده‌های جدید تعمیم یابد.

هنگام آموزش مدل، اگر مدل از الگوریتم‌های پیچیده استفاده کند، ممکن است به نویز موجود در داده‌های آموزشی حساس شود. از این‌رو،  Regularization کمک می‌کند تا توجه مدل به نقاط قوت اصلی داده‌ها معطوف شود و از یادگیری الگوهای غیردقیق یا نویزها صرفنظر کند. مدل‌های رگولاریزه‌شده معمولاً در برابر تغییرات کوچک در داده‌های ورودی مقاوم‌تر هستند. این پایداری به تعمیم‌پذیری بالاتر منجر می‌شود، یعنی مدل می‌تواند در شرایط مختلف و در داده‌های غیرآموزشی نیز عملکرد خوبی داشته باشد.

از طرفی، به مدل این امکان را می‌دهد که بین دقت بر روی داده‌های آموزشی و عملکرد بر روی داده‌های جدید یک تعادل مناسب برقرار کند. به عنوان مثال، در یک مسئله طبقه‌بندی تصاویر، اگر یک مدل عمیق بدون Regularization آموزش ببیند، ممکن است به شدت به ویژگی‌های خاص تصاویر آموزشی وابسته شود، مانند پس‌زمینه یا نورپردازی خاص. با اضافه کردن رگولاریزیشن، مدل مجبور می‌شود تا نسبت به این عوامل حساسیت کمتری داشته باشد و بتواند ویژگی‌های عمومی‌تری را شناسایی کند که در تصاویر دیگر (که شاید پس‌زمینه یا نورپردازی متفاوتی دارند) نیز قابل استفاده هستند.

نحوه عملکرد تکنیک regularization چگونه است؟

همانگونه که پیشتر هم صحبت شد، آموزش یک مدل، با یک مقدار تصادفی اولیه وزنها آغاز و در طول فرآیند آموزش، تابع هزینه مسئول به‌روزرسانی این وزنها در جهت رسیدن به خطای تا حد ممکن نزدیک به صفر، می‌باشد و  این فرآیند در نهایت، با هدف یافتن یک مرز  تفکیک‌کننده میان داده‌های کلاس‌های مختلف، پیش خواهد رفت. اما همانگونه که میدانیم، نه یک مرز منحصر‌به فرد، بلکه مرزهای متعددی قابل ترسیم و دست‌یافتنی است که هر یک از آنها هدفی را دنبال می‌کنند و مزایا و مشکلاتی را با خود به‌همراه دارند. آنچه که در این میان، ارزشمند است و نکته طلائی به‌شمار می‌آید این است که این مرز، منجر به پدیده overfitting نشود. یعنی مرزی بدست نیاید که روی داده‌های آموزش بسیار عالی، اما روی داده‌های جدید با نتیجه غیر قابل قبول مواجه گردیم و به عبارتی مدل، تعمیم ‌پذیری پایینی داشته باشد.

می‌دانیم که بردارهای وزن، در طول آموزش، توسط تابع هزینه به‌روز می‌شوند و عملا مقادیر بدست آمده توسط تابع هزینه، متاثر از  تغییرات ایجاد شده در پارامتر بردار وزن مربوط به ویژگی‌ها می‌باشند.

از طرفی، نتایج نشان دادند، هنگامیکه overfitting رخ می‌دهد، بردار وزنها دارای مقادیر عددی نسبتا بزرگ هستند. این نتیجه، به عنوان یک دانش کلیدی محسوب می‌شود که می‌تواند به عنوان یک شرط، عنان تابع هزینه را در دست گیرد و مانند یک مسئله بهینه‌سازی با آن برخورد شود. در واقع ما این دانش را به یک penalty term یا regularization term مبدل می‌سازیم که در کنار رابطه مربوط به تابع هزینه قرار گرفته، محدودیتی برای او ایجاد می‌کند به این صورت که، یافتن مقدار کمینه خطا را، به استفاده از مقادیر بهینه پارامتر مربوط به بردار وزن، مشروط می‌سازد.

بنابراین، ما به جای ا ستفاده از تابع هزینه به تنهایی، یک ترم جدید به آن اضافه می‌کنیم و اینگونه آن را به ازای مقادیر کوچکی از وزنها، محدود می‌سازیم. زیرا بطور کلی این تابع، تمایل به رسیدن به مقدار کمینه دارد و نمی‌پذیرد که بخشی از این ترم، با مقادیر بزرگ، همچون سدی او را در رسیدن به هدفش، مانع گردد. طبق این استدلال، می‌توان تابع هزینه را به‌گونه‌ای دیگر، با درنظر گرفتن این دانش، بصورت زیر بازنویسی کرد.

Cost = Loss function + λ . Regularization term

در این رابطه‌ی جدید، λ نقش همان افساری را بازی خواهد کرد که با ضرب در اندازه بردار وزن، او را به سمت مقادیر کوچک، هدایت خواهد کرد.

چگونه می‌توانیم به کمک روابط ریاضیاتی، Regularization term  را با هدف تعیین شده، خلق کنیم؟

همانطور که میدانیم، تابع هزینه و ترم مربوط به آن، انتخابی است که بسته به نوع مسئله تبیین، و مورد استفاده قرار می‌گیرد. اما Regularization term یا عبارت جریمه‌ای که قرار است موجب ایجاد محدودیت، برای تابع هزینه شود چطور؟ چگونه دانش مذکور را به یک عبارت ریاضی مبدل و مورد استفاده قرار دهیم؟

در ریاضیات، مفهومی وجود دارد به نام  نرم (Norm) که برای اندازه‌گیری بزرگی، یا طول یک بردار در فضاهای مختلف، مورد استفاده قرار می‌گیرد. نرم به ما کمک می‌کند تا تشخیص دهیم که یک بردار چقدر بزرگ، و از چه ویژگی‌هایی برخوردار است. نرم‌ها، به ما اجازه می‌دهند که اطلاعات دقیقی درباره ترکیب‌های مختلف بردارها، فضاها و تحلیل‌های پیشرفته‌ی آماری به دست آوریم. آنچه که ما می‌دانیم این است که می‌خواهیم، بردار وزن‌های ما، تا حد ممکن، با مقادیر کوچک مقداردهی شوند. بنابراین، می‌توان از رابطه ریاضی نرم کمک گرفته، و اندازه یا بزرگی بردار وزن را با ضرب در یک ضریب(λ)، کوچک نگه داشت. همانگونه که در رابطه بالا نشان داده شد،  λ یک پارامتر تنظیم (hyperparameter) است که میزان شدت جریمه را کنترل می‌کند. وجود این ترم باعث کاهش وزن‌های بزرگ می‌شود، زیرا اگر وزن بزرگی داشته باشیم، جریمه آن بزرگ می‌شود و این ویژگی با خواست معین تابع هزینه در تناقض است. به این ترتیب ما با این ضریب، وزن‌ها را متمایل به کوچک‌تر شدن خواهیم کرد.

در ریاضیات و به خصوص در تحلیل عددی و هندسه، انواع مختلفی از نرم‌ها وجود دارد که هر یک از آنها، ویژگی‌های خاص خود را داشته و در زمینه‌های مختلف ریاضی، آمار و یادگیری ماشین کاربرد دارند. در ادامه به معرفی دو نوع از مهمترین انواع نرم‌ها به همراه تاثیری که هر یک از این دو نوع انتخاب می‌تواند روی پارامتر مربوط به بردار وزن بگذارند، صحبت خواهیم کرد.

– L1 norm یا (Lasso)

نرم 1، مجموع مقدار مطلق تمام مؤلفه‌های بردار را محاسبه می‌کند. به طور هندسی، نرم 1 نشان‌دهنده فاصله طولی از مبدأ تا نقطه x ، با حرکت در راستای محورهای مختصاتی (شبیه حرکت در یک شبکه) است. این نوع نرم، حساس به مؤلفه‌های فردی است و از آنجائیکه طبق شکل زیر، نقاط برخورد نزدیک به محورهای مختصات می‌افتد، می‌تواند باعث صفر شدن وزن برخی ویژگی‌ها شده، و به انتخاب ویژگی‌ها کمک و مدل را ساده‌تر ‌کند. نرم 1 نیز برای بهینه‌سازی و در الگوریتم‌های یادگیری ماشین به کار می‌رود، اما در شرایطی که، قصد ما داشتن یک شبکه  با کمترین اندازه یا sparcity باشد.

–  L2 norm یا نرم اقلیدسی(Ridge)

نرم2 ، برابر با جذر مجموع مربع‌های تمام مؤلفه‌های بردار است. به طور هندسی، نرم 2 فاصله عمودی از مبدأ (نقطه صفر) تا نقطه x  در فضای n بعدی را نشان می‌دهد. این نوع نرم، به ویژه در مسائل بهینه‌سازی و یادگیری ماشین مورد استفاده قرار می‌گیرد و موجب smoothness  می‌شود، به این معنی که به تغییرات نرمال و یکنواخت در وزن‌ها حساس است و در عین حال، با قرار دادن وزنها در یک رنج مشخص(با توجه به ضریبی که تعیین میکنیم) از تمام نودهای شبکه در تصمیم‌گیری استفاده نموده و هیچ یک را غیرفعال(صفر) نمی‌کند. شکل زیر، رابطه‌ی میان تابع هزینه و هر یک از این نوع نرم‌ها را نشان می‌دهد:

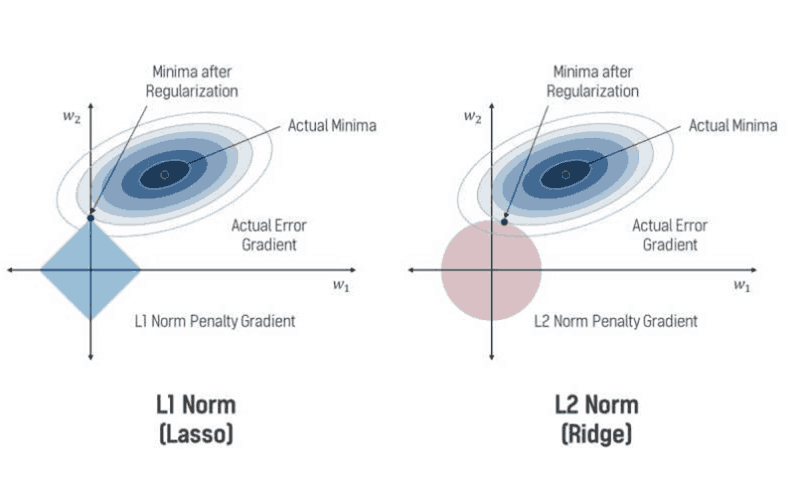
L1-norm vs l2-norm in regularization

مقایسه و  انتخاب میان دو نوع نرم در regularization

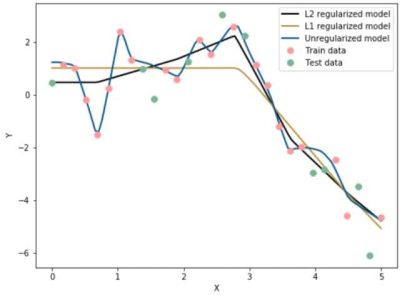
همانطور که شرح داده شد، هر یک از این نوع نرم‌ها می‌توانند با توجه به هدف تعیین شده، مورد استفاده قرار گیرد. بطور مثال، اگر هدف داشتن یک شبکه sparce است که تمام نودها در تعیین خروجی نقش نداشته باشند، می توانیم از نرم 1 استفاده نمائیم. زیرا به عنوان نمونه، در شکل بالا، با فرض داشتن دو مولفه برای بردار وزن و ترسیم آن در فضای دو بعدی، از روی رابطه ریاضی نرم 1 و محاسبه مقدار مطلق مولفه‌های مربوط به بردار وزن، احتمال برخورد تابع هزینه با نرم 1 بردار وزن، در نقاطی نزدیک به محور مختصات امکان‌پذیر است. بنابراین در نقطه تلاقی، در کنار داشتن مقدار بهینه تابع هزینه،  این مقدار از روی کمترین مقدار بردار وزن نیز بدست می‌آید، از طرفی، یکی از این بردارها مقدار صفر برمیگزیند و به عبارتی غیرفعال شده و شبکه   sparceتر خواهد شد.

اما اگر مدل به تغییرات نرمال و یکنواخت در وزن‌ها حساس و در عین حال، با قرار دادن وزنها در یک رنج مشخص(با توجه به ضریبی که تعیین میکنیم) از تمام نودهای شبکه بخواهیم در تصمیم‌گیری استفاده نمائیم، از نرم 2 استفاده می‌کنیم. طبق رابطه ریاضی مربوط به نرم 2،  تابع هزینه، با کمترین مقدار وزنها(شعاع کمینه در دایره) در هر یک از نقاط مربوط به دایره ترسیم شده در شکل، به مقدار بهینه دست می‌یابد بدون آنکه بخواهیم برخی از ویژگیها را با مقادیر صفر، غیرفعال سازیم.

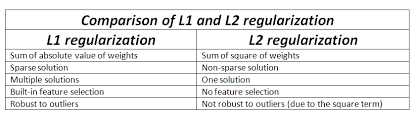
با توجه به اینکه، در مسیر bachward، به کمک گرادیان از تابع هزینه کل(بازنویسی شده)، این به‌روزرسانی‌ها صورت می‌گیرد، به لحاظ راحتی در مشتق‌گیری و با هدف استفاده از تمام ویژگی‌‌ها، انتخاب برتر در اکثر مواقع، نرم 2 می‌باشد. در کتابخانه پایتورچ نیز، از این نوع نرم استفاده شده است که در ادامه، بیشتر به نحوه پیاده‌سازی این تکنیک به کمک کتابخانه پایتورچ می‌پردازیم.

پیاده سازی تکنیک Regularization  در پایتورچ

مانند تکنیک‌های قبلی، ما دو راه برای پیاده‌سازی این تکنیک‌‌ داریم: بصورت دستی یا به کمک متدهای آماده در کتابخانه قدرتمند پایتورچ. در ادامه، هر دو رویکرد پیاده‌سازی این تکنیک را مورد بررسی قرار خواهیم داد.

• پیاده‌سازی تکنیک Regularization به روش دستی در پایتورچ

در روش دستی، کافیست ابتدا یک تابع، به منظور محاسبه نرم 2 یک بردار تعریف نمائیم. سپس این تابع را در کنار تابع هزینه تعریف شده، فراخوانی نموده و اینگونه یک تابع هزینه با درنظر گرفتن Regularization penalty term، حاصل میگردد. ما می‌توانیم ضریب کنترلی میزان جریمه یا همان λ را در رابطه تابع هزینه، به عنوان ضریب تابع جریمه، بگنجانیم. کد مربوط به این نوع پیاده‌سازی(دستی) بصورت زیر می‌باشد که ابتدا تابع مربوط به نرم 2  بصورت زیر تعریف می‌شود.

Python

 def l2_penalty(w):
     return (w ** 2).sum() / 2

لازم به ذکر است که  در این رابطه، با توجه به اینکه در هنگام گرادیان‌گیری، ضرایب حذف خواهند شد، با گذاشتن یک ضریب معادل 2/1، از محاسبه ریشه دوم در رابطه نرم 2 به منظور محاسبه‌ی اندازه بردار، بی‌نیاز خواهیم شد.

بنابراین بخش دوم کار، تعریف تابع هزینه جدید، با در نظر گرفتن Regularization penalty term، می‌باشد.

Python

def loss(self, y_hat, y):
     return (loss(y_hat, y)+ self.λ * l2_penalty(self.w))

که در این رابطه و تابع هزینه کل، مقدار ضریب جریمه یا همان λ، توسط کاربر تنظیم می‌گردد و در فرآیند آموزش شبکه، از این تابع هزینه در به‌روزرسانی وزن‌ها، استفاده می‌شود.

• پیاده‌سازی تکنیک Regularization به کمک متد آماده در پایتورچ

همانگونه که در روش دستی مشاهده شد، ضریب جریمه به عنوان یک ورودی، توسط کاربر تنظیم و به بدنه برنامه ارسال می‌شود. در کتابخانه پایتورچ، متد آماده‌ای به منظور محاسبه نرم 2 یک بردار وجود دارد. به منظور اعمال این تکنیک، کافیست هنگام تعیین نمودن optimizer مورد نظر، در کنار دادن مقدار نرخ یادگیری و … یک پارامتر ورودی به نام weight decay را که معادل همان ضریب جریمه(λ) است مقداردهی نمائیم. این پارامتر، بطور پیش‌فرض، مقدار آن صفر می‌باشد. در صورتیکه ما به آن یک مقدار عددی منتسب کنیم، بطور خودکار، تکنیک Regularization با ضریب ارائه شده، روی مدل اعمال میگردد. در واقع در صورتیکه در یک مقاله در مورد استفاده از تکنیک Regularization سخن به میان می‌آید، میتوان به همین سادگی، این تکنیک را با مقداردهی به این پارامتر ورودی یعنی weight decay، اعمال نمود که اینگونه، با ایجاد یک محدودیت در به‌روزرسانی مقادیر وزنها، در تابع هزینه، علاوه بر جلوگیری از پدیده overfitting به generalize کردن مدل نیز کمک می‌شود.

Python

optimizer = optim.Adam(params = mdl.parameters(),lr = lr, weight_decay = 0.001)

درپایان این سری از پست‌ها، که با عنوان تکنیک‌های generalization مدل‌های یادگیری عمیق مورد بررسی قرار گرفتند، نکته‌ای وجود دارد که هنگام استفاده از این تکنیک‌‌ها، بهتر است مدنظر قرار گیرند. هر یک از این چهار تکنیک، با نام‌های Dropout، Batch Normalization، Early Stopping و Regularization در کنار اینکه می‌توانند مدل‌های یادگیری عمیق را بهبود بخشند، بسیار بستگی به تمورد استفاده دارند. بنابراین شاید بتوان گفت، پیش از استفاده از این تکنیک‌ها، بهتر است در مورد میزان تاثیر آنها با توجه به دیتاست مورد نظر، بررسی‌های لازم انجام، سپس اقدام به افزودن این تکنیک‌ها نمائیم.