پارامترهای ماشین بردار پشتیبان

ماشین بردار پشتیبان(support vector machine)

همانطور که میدانیم SVM اولین بار توسط آقای Vapnik برای مسائل طبقه بندی خطی دو کلاسه ارائه شد. بعدها این الگوریتم برای مسائل طبقه بندی غیرخطی و همچنین مسائل رگرسیون تعییم یافته شد. اگر شناخت کاملی نسبت به SVM در مسائل طبقه بندی و رگرسیون ندارید، پیشنهاد میکنیم قبل مطالعه این پست، مطلب مربوط به ماشین بردار پشتیبان در مسائل طبقه بندی و رگرسیون را مطالعه کنید.

مرور مختصر بر SVM

هدف SVM در مسائل طبقه بندی پیدا کردن بهترین مرز ممکن بین داده های دو کلاس است. برای اینکار آقای Vapnik یک تابع هزینه ای همراه با یک سری قیدهایی در نظر گرفته  است. در این مسئله بهینه سازی هدف این است که مرزی بین دو گروه بدست بیایید که حداقل خطای ممکن را داشته باشد و از طرفی به طور صریح در مسئله بهنیه سازی بیان شده که مرز باید بیشترین فاصله را بین دو گروه داشته باشد. همین باعث شده که الگوریتم SVM بهترین مرز ممکن بین دو گروه را پیدا کند. و از آنجا که برای پیدا کردن مرز از بردارهای پشتیبان استفاده میکند، باعث میشود که در ابعاد بسیار بالا هم خیلی خوب عمل کند در حالی که الگوریتمهای دیگه چنین قابلیتی ندارند.

پارامترهای SVM

ماشین بردار پشتیبان یک سری پارامترهایی دارد که باید توسط کاربر تعیین شوند. این پارامترها نقش اساسی در عملکرد SVM دارند و اگر ما شناخت درستی از این پارامترها نداشته باشیم، مطمئنا مقادیر مناسبی هم برای آنها تعیین نخواهیم کرد و در نتیجه SVM خوب عمل نخواهد کرد.  ما برای رسیدن به بهترین عملکرد SVM لازم است که مقادیر مناسبی برای پارامترهای آن در نظر بگیریم. ماشین بردار پشتیبان به طور کلی یک پارامتر اساسی برای حالت خطی (C یا همان هزینه) و دو تا پارامتر اساسی برای غیرخطی ( C و پارامتر مرتبط با کرنل غیرخطی) دارد.

پارامتر C در SVM

پارامتر C یک ترم ثابت مثبت است که توسط کاربر تعیین می‌شود. برای درک بهتر نقش پارامتر C در مسئله بهینه سازی SVM ، ابتدا بیایید مسئله طبقه بندی زیر را در نظر بگیریم:

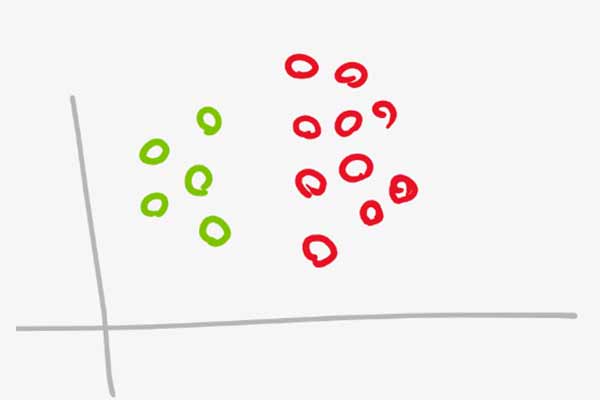
همانطور که میبنیم یک مسئله طبقه بندی خطی دو کلاسه هست که داده های دو گروه کاملا از هم تفکیک شده اند. برای حل چنین مسائلی آقای Vapnik الگویتم hard margin SVM  را مطرح کرد.

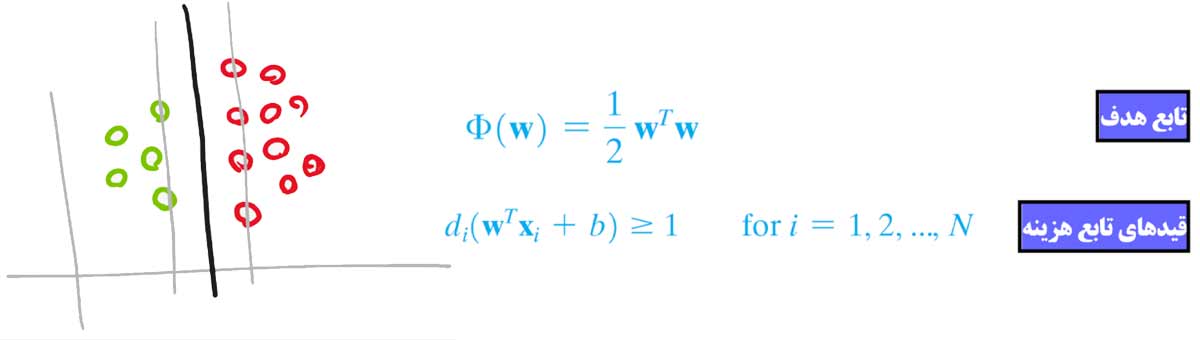
مسئله بهینه سازی این الگوریتم طوری تعریف شده است که الگوریتم مرزی پیدا کند که اولا خطای طبقه بندی صفر روی داده های آموزش داشته باشد و از طرفی بیشترین فاصله(مارجین) را نسبت به نزدیکترین نمونه های دو کلاس(بردارهای پشتیبان) داشته باشد. قیدها بسیار شدید هستند و باید مرزی پیدا شود که در آن حتما خطای طبقه بندی صفر باشد!  این مسئله بهینه سازی در دو جا به مشکل میخورد!

مشکل اول hard margin SVM

اگر همانند شکل زیر نمونه های دو گروه داده آموزش کاملا تفکیک پذیر نباشند الگوریتم SVM  همگرا نخواهد شد. چون قیدها بسیار شدید هستند و مدل زمانی به یک جواب همگرا میشود که خطا صفر شود که در اینجا عملا امکان پذیر نیست.

مشکل دوم hard margin SVM

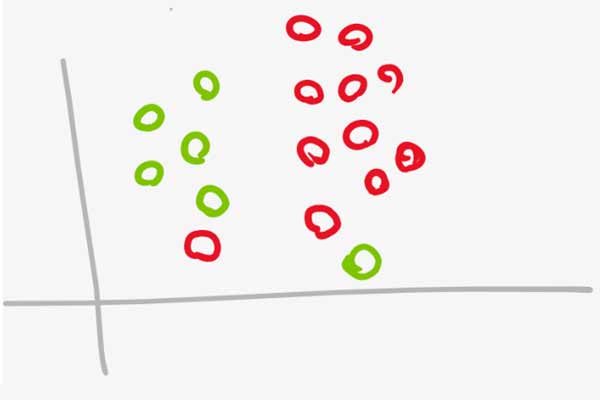
اگر داده های دو گروه همانند شکل زیر باشند، مسئله بهینه سازی به خاطر داشتن قیدهای بسیار شدید مرز مناسبی پیدا نخواهد کرد. همانطور که میبنید مرز مناسب به صورت آبی رنگ است ولی مرزی که SVM پیدا میکند (رنگ مشکی) مناسب نیست. درسته که این مرز بدست آمده توسط SVM در داده آموزش خطای صفر خواهد داشت، ولی در داده جدید خوب عمل نخواهد کرد. به عبارتی SVM روی داده آموزشی Overfit  شده است!

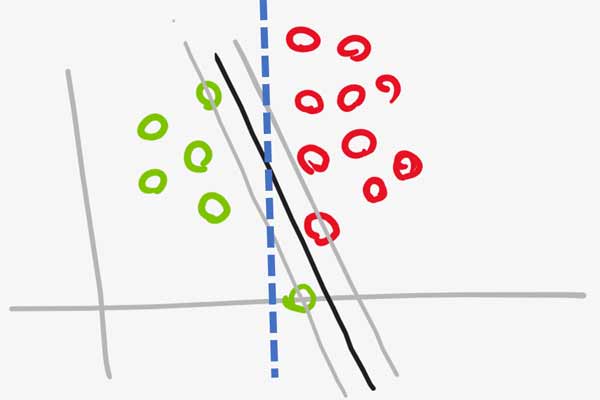
راهکار soft margin SVM

برای حل این مسئله آقای  Vapnik از یک متغیر مجازی(slack variable)  کمک گرفت.

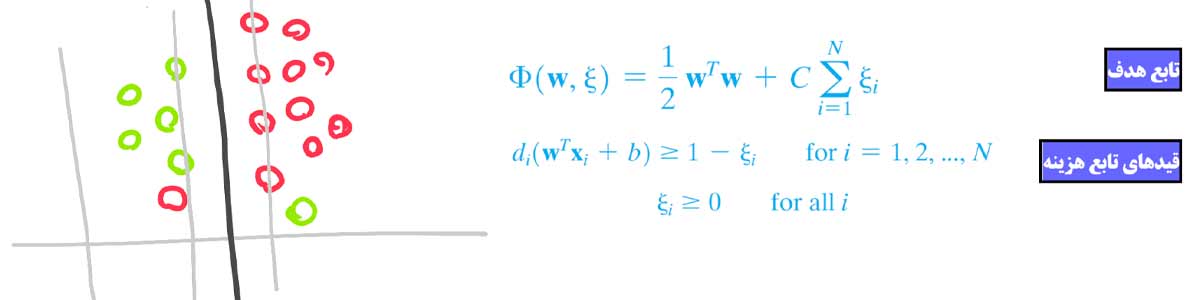
اگه خیلی ساده به مسئله نگاه کنیم، آقای Vapnik مسئله بهینه سازی رو طوری تغییر میدهد که مدل اجازه داشتن کمی خطا در محاسبه مرز داشته باشد. به عبارتی شدت قیدها را کاهش می دهد و به مدل اجازه میدهد که مقداری خطا داشته باشد.

نقش پارارمتر C در SVM

پارامتر C یک ترم ثابت مثبت است که توسط کاربر تعیین می شود و Margin را کنترل می کند.

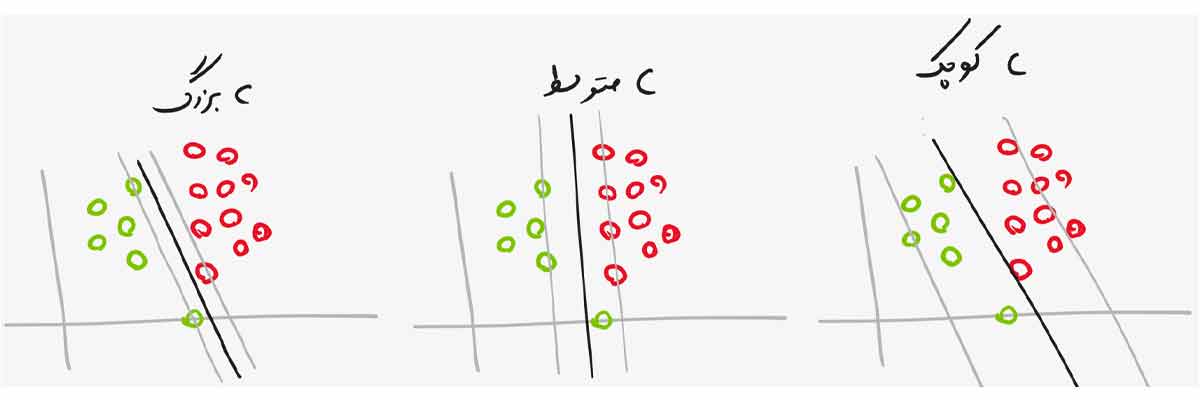
•  Cبزرگ: C اگر مقدار بزرگی داشته باشد در نتیجه آن قیدهای مسئله بهنیه سازی SVM شدید می شوند و اگر خیلی خیلی بزرگ باشد، مسئله بهینه سازی شبیه Hard Margin می شود. یعنی خطای طبقه بندی باید صفر باشد!
• C متوسط: C اگر مقدار متوسط و حد معمولی داشته باشد در نتیجه آن شدت قیدهای مسئله بهنیه سازی SVM کمتر می شود و به مدل اجازه میدهد مقداری خطا داشته باشد (ولی خطای حداقل نه خیلی زیاد) و همین باعث میشود که مرز مناسبی برای مسئله طبقه بندی پیدا کند.
• C کوچک: C اگر مقدار کوچکی داشته باشد در نتیجه آن شدت قیدهای مسئله بهنیه سازی SVM خیلی کمتر می شود و به مدل اجازه میدهد خطای زیادی داشته باشد که در نتیجه آن ممکن است مدل به outlierها حساس شود و در نتیجه مرز مناسبی بدست نیاید. مقدار C نباید خیلی کوچک باشد!

ما با نقش پارامتر C در مسائل طبقه بندی خطی آشنا شدیم و بهتر است بدانیم که در مسائل طبقه بندی غیرخطی و یا رگرسیون خطی و غیرخطی چنین نقشی را دارد.

ماشین بردار پشتیبان در مسائل غیرخطی

همانطور که میدانیم SVM برای حل مسائل غیرخطی، داده را با کمک کرنلهای غیرخطی به فضای خطی نگاشت داده و در آن فضای خطی مرز بهینه خطی را پیدا میکند که معادل مرز غیرخطی در فضای اصلی غیرخطی است. برای اینکار کرنلهای مختلفی وجود دارد که معروفترین آنها Radial Basis Function(RBF) هست. این کرنل طبق رابطه زیر داده را به فضای غیرخطی نگاشت می دهد.

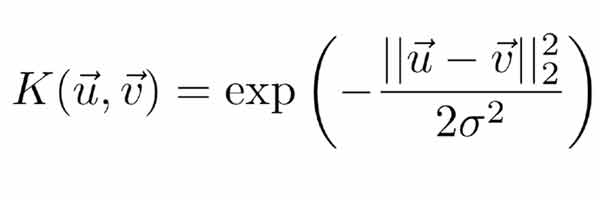
پارامتر سیگما در SVM غیرخطی

همانطور که در رابطه rbf میبینید در این رابطه پارامتری به نام سیگما وجود دارد که یک مقدار ثابت مثبت هست و توسط کاربر مشخص می‌شود. پارامتر سیگما به همراه پارامتر C نقش کلیدی در عملکرد SVM غیرخطی دارند. در مورد نقش C صحبت کردیم و الان میخواهیم نقش پارارمتر سیگما را متوجه شویم.

برای درک بهتر نقش سیگما اجازه بدهید یک مثال ساده بزنیم. فرض کنید که یک داده دو کلاسه غیرخطی به صورت زیر داریم، و میخواهیم این داده را به فضای خطی نگاشت دهیم.

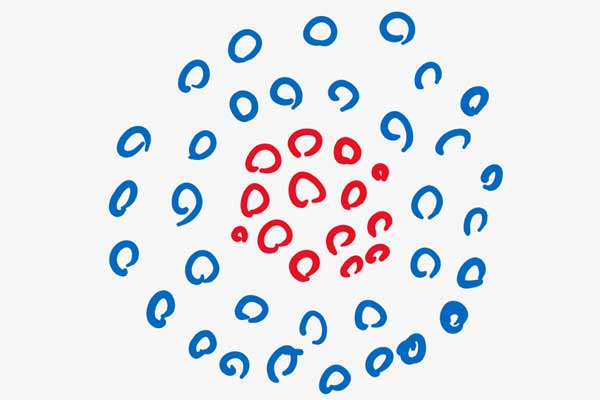
فرض کنید ما میخواهیم یک نقطه در فضای ویژگی در نظر بگیریم و بعد فاصله تمامی نمونه ها را نسبت به آن محاسبه کنیم . اینم فرض کنید همانند شکل زیر فاصله اقلیدسی نقطه مرکزی تا مرز r هست.

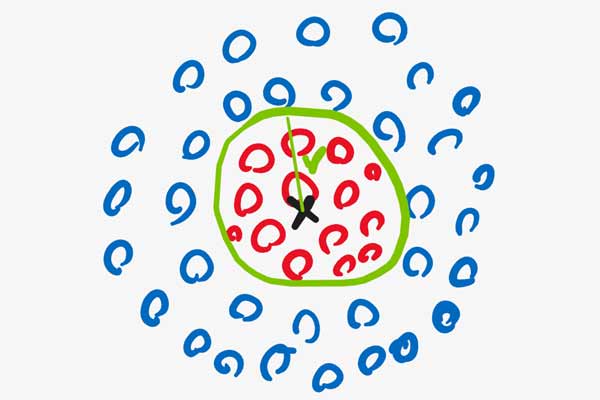
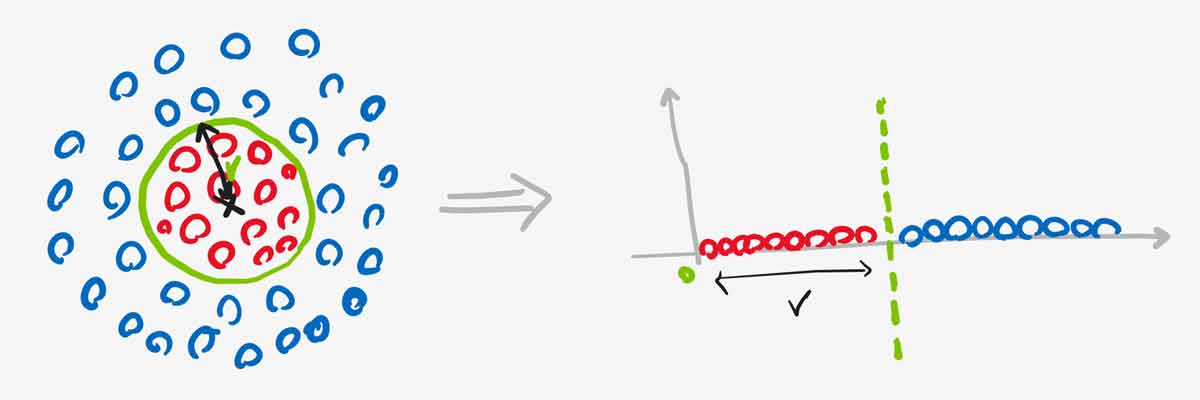
حال اگر فاصله اقلیدسی تک تک نمونه ها را نسبت به نقطه مرکزی حساب کنیم و از آن به عنوان مقدار هر نمونه در فضای جدید استفاده کنیم، در این صورت همانند شکل زیر داده ها را به یک فضای خطی یک بعدی نگاشت خواهیم داد. در این فضا داده ها به صورت خطی تفکیک پذیر هستند.

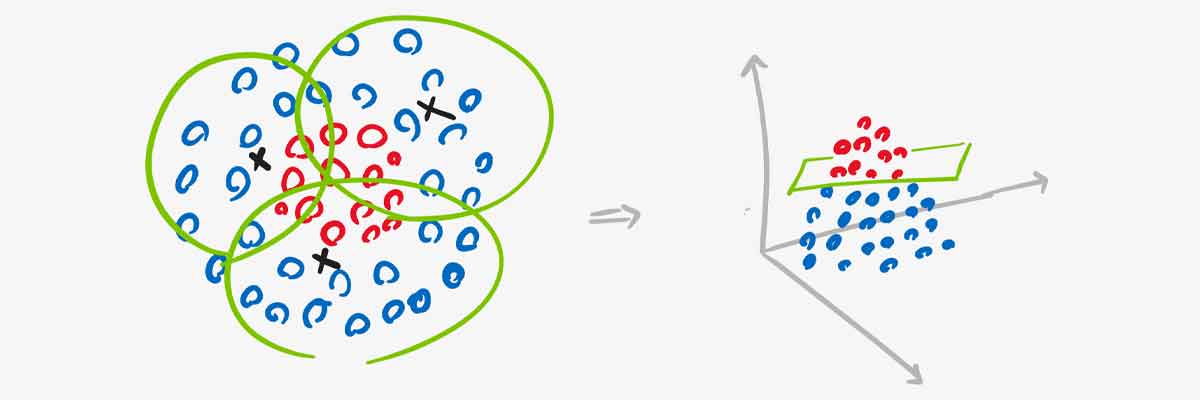
واقعیت این است که در عمل فقط با یک نقطه مرکزی نمیتوان داده ها را به یک فضای خطی نگاشت داد. لازم است که تعداد نقاط را بیشتر بکنیم. و هر نقطه ای باید یک بخشی از فضای ویژگی را حول خودش پوشش بدهد. برای مثال فرض کنید ما سه نقطه در نظر گرفته ایم و هر کدام همانند شکل زیر ناحیه ای در یک شعاعی را پوشش داده اند. حال اگر فاصله تک تک نقاط را نسبت به سه تا نقطه حساب کنیم، فضای جدید یک فضای سه بعدی خطی خواهد بود، چرا که تعداد نقاط 3 هست و به ازای هر نمونه ورودی سه تا مقدار بدست می آید. هر چقدر تعداد نقاط بیشتر شود، ابعاد فضای جدید بیشتر خواهد شد.

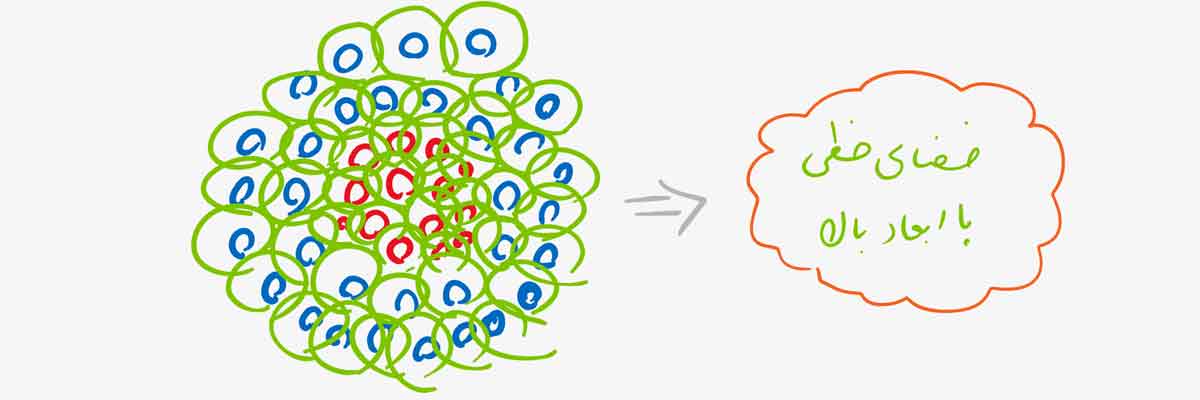
هر کدام از این نقاط به نوعی یک کرنل غیرخطی هستند و اینکه هر نقطه مرکزی چقدر از همسایگی خودش را پوشش دهد بستگی به مقدار سیگمای کرنل دارد که توسط کاربر مشخص می‌شود.

اگر مقدار سیگما به درستی تعیین نشود داده به خوبی به فضای جدید نگاشت داده نمی‌‎شود و در نتیجه در فضای جدید داده خطی نخواهد بود و مرز مناسبی برای داده بدست نخواهد آمد. سیگما در کرنل RBF چنین نقشی دارد و مشخص می‌کند که هر کدام از نقاط چه فضایی از داده ورودی را پوشش بدهند.

جالب است که بدانید در SVM تک تک داده های آموزشی یک کرنال هستند و همین باعث می شود که SVM داده غیرخطی را از یک فضای غیرخطی با بعد پایین به یک فضای خطی با بعد بالا نگاشت دهد.

چطور مقادیر مناسب برای پارامتر C و سیگما تعریف کنیم؟؟

اینکه چه مقادیری برای پارامترهای C و سیگما تعریف کنیم کاملا بستگی به شرایط هر پروژه دارد. و نمیشه مقادیر خاصی را عنوان کرد که در همه پروژه ها مناسب باشند. باید در هر پروژه ای با کمک روش Cross validation مقادیر مناسب برای پارامترهای SVM پیدا کنیم.

اگر قصد یادگیری تخصصی الگوریتم SVM هستید پیشنهاد میکنیم که فصل 4 دوره جامع شناسایی الگو-یادگیری ماشین را مشاهده کنید. در این فصل در ابتدا تئوری و ریاضیات SVM از پایه آموزش داده شده، سپس به صورت مرحله به مرحله پیاده سازی شده و در نهایت در پروژه های عملی استفاده شده است.