گرادیان نزولی و نقش آن در فرایند یادگیری شبکه های عصبی
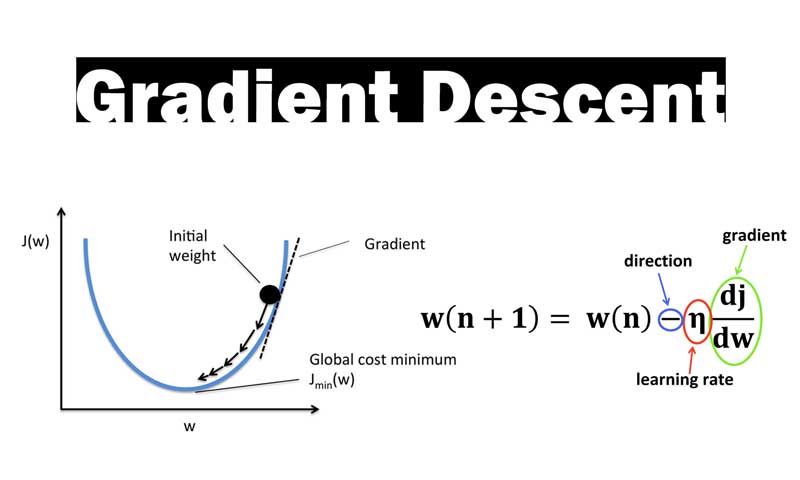
گرادیان نزولی (gradient descent) یک الگوریتم بهینه سازی است که در شبکه های عصبی با کمک آن وزنهای سیناپسی تنظیم می شوند. به عبارتی با کمک گرادیان نزولی، شبکه های عصبی آموزش دیده و دانش لازم برای حل مئسله را بدست می آوردند. این الگوریتم با یک مقدار اولیه برای پارامتر بهینه سازی (وزنهای سیناپسی در شبکه های عصبی) شروع میکند، و براساس شیب خطا پارامتر بهینه سازی را تنظیم میکند. گردایان نزولی در طول تکرارهای مختلف، در جهت شیب منفی خطا حرکت میکند تا به نقطه بهینه (global minima) همگرا شود. با کمک این رویکرد، شبکه های عصبی، در طول زمان وزنهای سیناپسی خود را برای حل مسئله خاص تنظیم میکنند. در این پست میخواهیم با فلسفه گرادیان نزولی برای حل مسئله، و چالشهایی که دارد آشنا شویم.
گرادیان نزولی
احتمالا خیلی از شماها هم مثل من با اصطلاح گرادیان نزولی در درس شبکه های عصبی آشنا شده اید. گرادیان نزولی یک روش بهینه سازی بدون قید است که در طول تکرارهای مختلف پارامتر/پارامترهای بهینه سازی مشئله را تنظیم میکند.
برای اینکه درک بهتری از این الگوریتم داشته باشیم، بیایید با یک مثال عملی ساده مباحث را پیش ببریم. فرض کنید، یک مسئله بهینه سازی داریم که در آن، x پارامتر بهینه سازی مسئله و y تابع هزینه مسئله است و رابطه زیر بین آنها برقرار است.
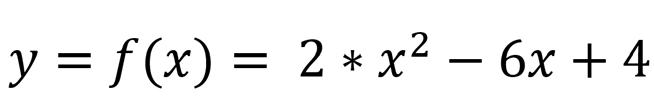
ما به ازای هر مقدار از x یک هزینه ای خواهیم داشت. اگر ما به x مقادیر مختلفی بدهیم و y را محاسبه کنیم میتوانیم یک نمودار همانند زیر رسم کنیم. در نمودار، به ازای مقادیر مختلف پارامتر بهینه سازی (x)، هزینه ی(y) متفاوتی داریم.
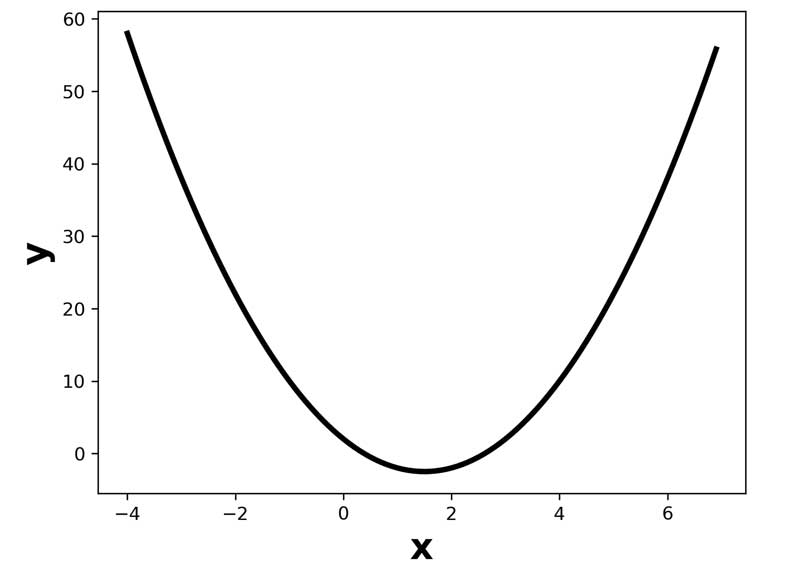
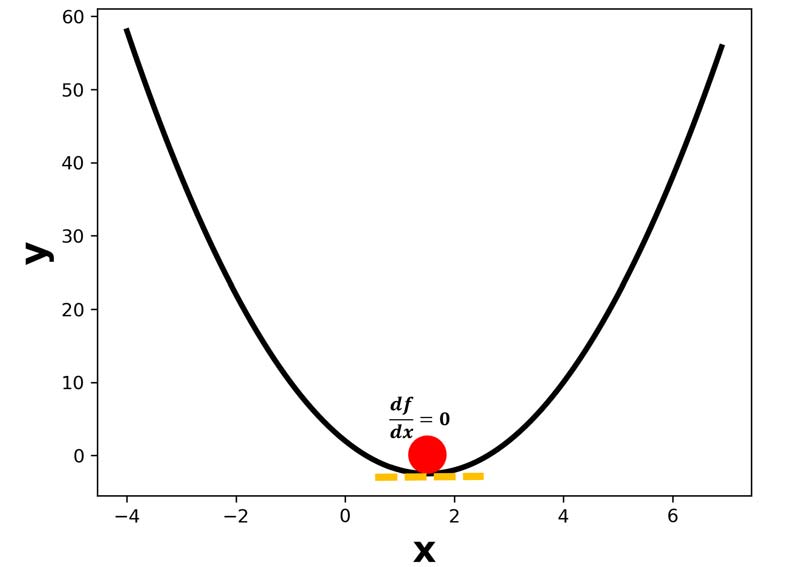
ما دنبال xی کمترین هزینه را داشته باشد. از لحاظ شکلی میتوانیم حدس بزنیم که x حدودا، 1.8 باشه به مقدار حداقل هزینه خواهیم رسید.
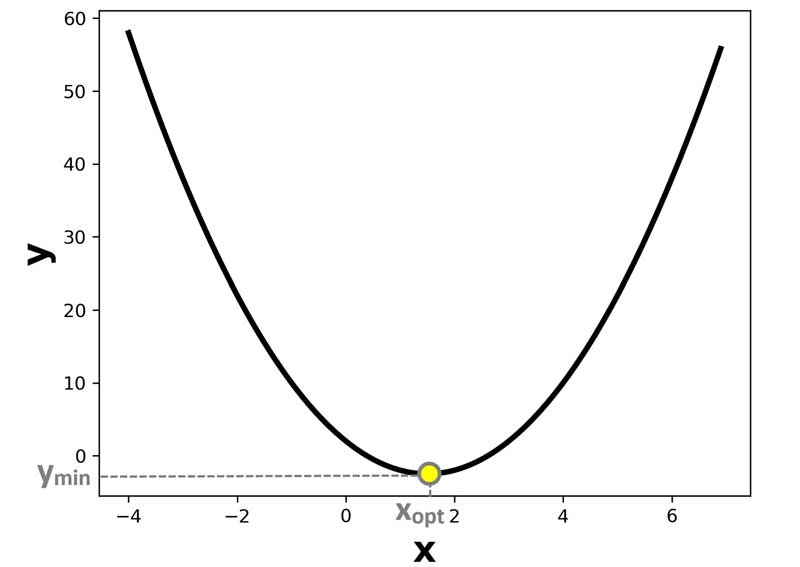
خب ما اینجا خیلی راحت به صورت چشمی متوجه شدیم که چه مقدار برای x باید در نظر بگیریم تا حداقل هزینه را داشته باشیم. ولی مسئله اینه که در مسائل عملی ابعاد بالا هست و رسم چنین نموداری امکان پذیر نیست، اونموقع باید چیکار کرد؟! خب پس باید الگوریتمی ارائه بدهیم که بتونه خودش مقدار بهینه را پیدا کند.
بیایید به نمودار بین پارامتر بهینه سازی و خطا نگاه کنیم. در شکل زیر، میزان تغییرات لحظه ای (شیب خطا) در چندین نقطه در روی منحنی مشخص شده است.
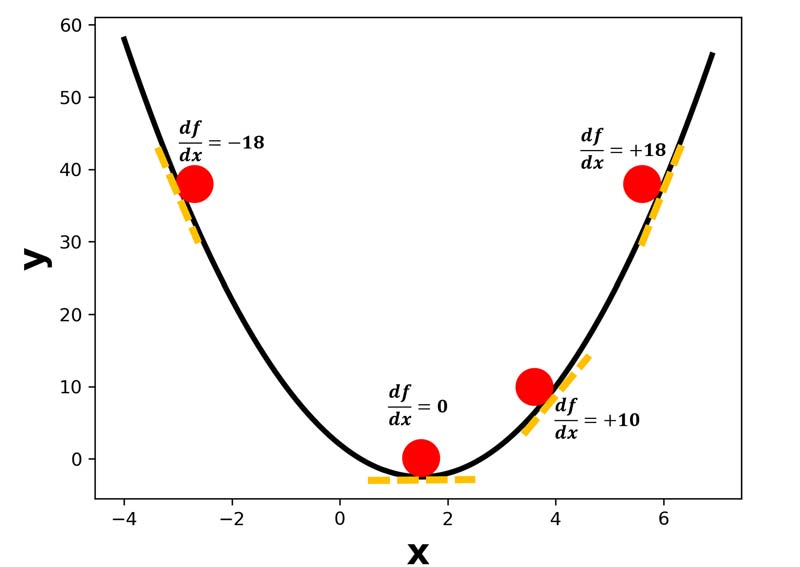
همانطور که در شکل مشخص هست، شیب منحنی در نقاط مختلف مقادیر مثبت یا منفی دارد و در یک نقطه، شیب منحنی برابر صفر هست و اون نقطه، نقطه بهینه ما هست. و میدانیم که میتوانیم با کمک مشتق، میزان تغییرات لحظه ای در هر نقطه از منحنی (شیب خطا در هر لحظه) را بدست بیاوریم.
پس برای پیدا کردن مقدار بهینه x، کافیه که از تابع هزینه نسبت به پارامتر بهینه سازی مشتق بگیریم و مساوی صفر قرار دهیم، مقداری که برای پارامتر بهینه سازی بدست میاید، مقدار بهینه ما است.
در شبکه های عصبی، به دلیل بالا بودن ابعاد (بعدا دقیقتر این مسئله را بررسی میکنیم)، و افزایش پیچیدگی محاسباتی نمیتوانیم این کار را انجام دهیم یعنی مقادیر بهینه را به یکباره بدست بیاوریم.
رویکرد گرادیان نزولی
گرادیان نزولی مطرح شده است تا این مسئله را در طول تکرارهای مختلف حل کند.گرادیان نزولی با یک مقدار اولیه برای پارامتر بهینه سازی شروع میکند و در طول زمان در جهت شیب منفی خطا حرکت میکند و پارامتر بهینه سازی را تنظیم میکند تا به مقدار بهینه برسد.
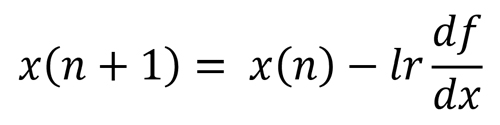
در این رابطه lr نرخ یادگیری هست و مقداری بین صفر تا یک هست. x(n) مقدار x در تکرار n است و x(n+1) مقدار x برای لحظه بعدی است که باید طبق رابطه تنظیم شود.
برای درک بهتر رویکرد همگرایی گرادیان نزولی، فرض کنید در ابتدا مقدار اولیه برای x برابر 3.8- است. حال میخواهیم با کمک گرادیان نزولی x را تنظیم کنیم. و به مقدار بهینه که حدودا 1.8 است، برسیم. یعنی جایی که شیب منحنی برابر صفر است.
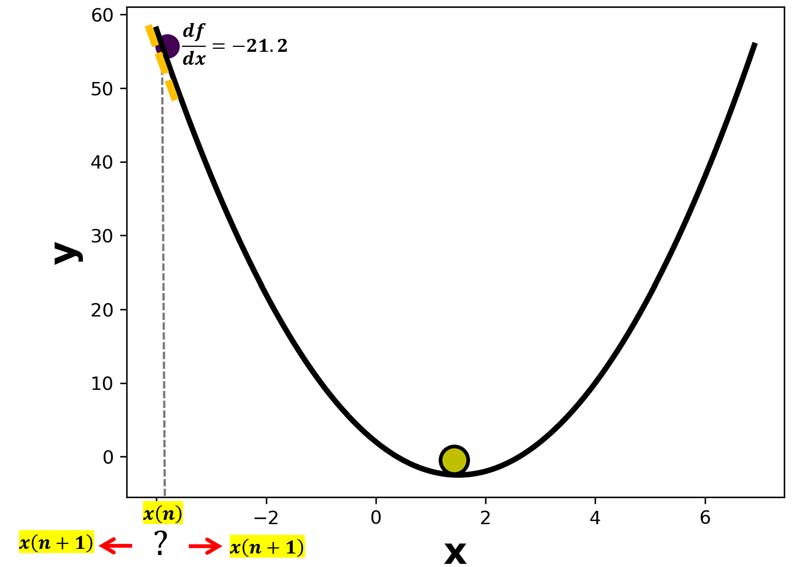
خب منطق چی میگه؟؟ منطق به ما میگه که x الان، مقداری کمتر از x بهینه است، برای همین، ما باید مقدار x را افزایش دهیم تا به نقطه بهینه نزدیک تر شویم. حال ببینیم که در گرادیان نزولی همچین اتفاقی میافته؟
خب اگر مشتق تابع هزینه نسبت به پارامتربهینه سازی محاسبه کنیم به رابطه زیر میرسیم. یعنی طبق رابطه زیر میتوانیم در هر لحظه شیب منحنی (تغییرات لحظه ای در هر نقطه از منحنی) را محاسبه کنیم.
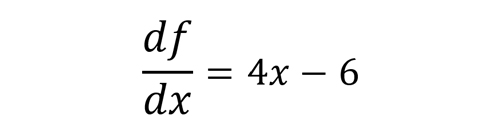
حال مشتق تابع هزینه در نطقه x=-3.8 برابر با 21.2- خواهد بود. یک مقدار منفی هست و اگر نرخ یادگیری هم برای مثال 0.05 باشد:
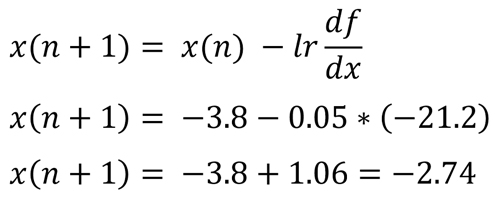
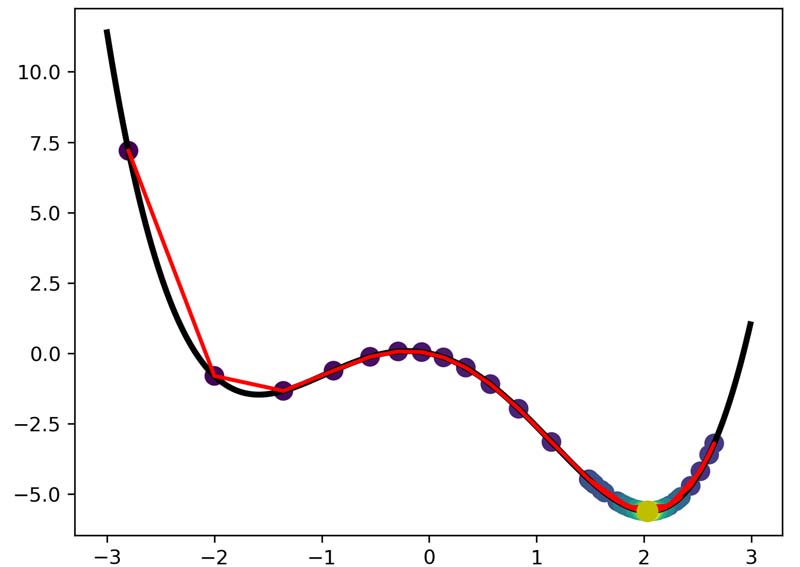
همانطور که دیدیم گرادیان نزولی، دقیقا انتظاری که ما داشتیم رو انجام داد و مقدار x را افزایش داد. این پروسه در هر تکرار انجام میشود تا x به مقدار بهینه برسد. از اونجا که شیب خطا در هر لحظه داره کم میشه، سرعت تغییرات هم رفته رفته همانند شکل زیر کمتر خواهد شد، تا اینکه بعد از چند تکرار شیب خطا صفر میشود و دیگر پارامتر بهینه سازی تغییر نمیکند و به عبارتی در نقطه بهینه همگرا می شود.
از کد زیر برای برای بهینه سازی مسئله مورد نظر استفاده کرده ایم:
Python
import torch from matplotlib import pyplot as plt f= lambda x:2*x**2-6*x+2 g= lambda x: 4*x-6 x=-3.8 lr=0.05 epoch=20 xn= [] yn=[] for iter in range(epoch): xn.append(x) yn.append(f(x)) gd= g(x) x= x - lr*gd xn= torch.tensor(xn) yn= torch.tensor(yn) plt.plot(x,f(x)+2,'oy',markeredgewidth=2,markersize=15,markeredgecolor='k')#+0.3 x= torch.arange(-4,7,0.1) y= f(x) gd= g(x) ind= torch.nonzero(gd==0) plt.plot(x,y,'k',linewidth=3) plt.xlabel('x',fontsize=20,fontweight='bold') plt.ylabel('y',fontsize=20,fontweight='bold') plt.plot(xn,yn+2,'--r') plt.scatter(xn,yn+2,s=150,c=xn) plt.show()
چالشهای گرادیان نزولی
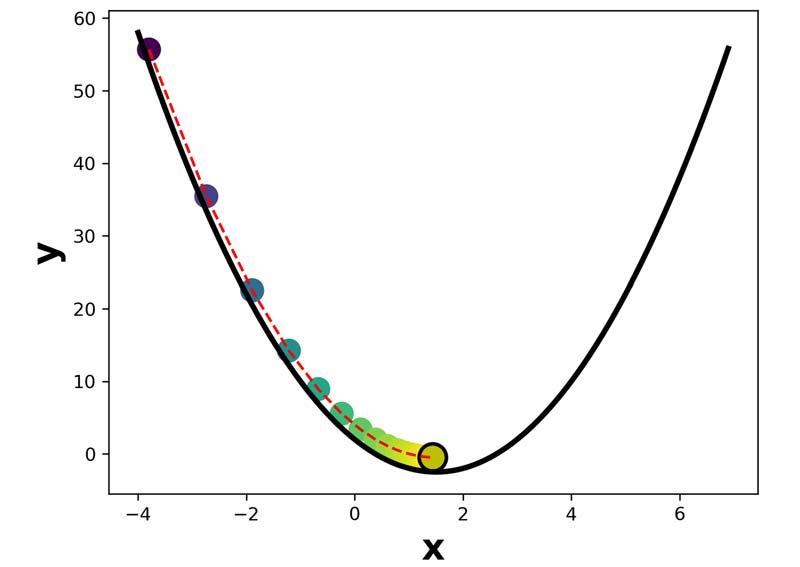
همانطور که صبحت کردیم، در گرادیان نزولی، در جهت شیب منفی خطا حرکت میکنیم تا به مقدار بهینه برسیم. یعنی جایی که شیبه خطا صفر باشد. ولی مسئله مهم اینه که در خیلی از مسائل واقعی، ما نقاط زیادی داریم که در آنها هم شیب خطا صفر است، ولی این نقاط لزوما نطقه بهینه نیستند و خطا در اون نقاط بالا هست. به این نقاط، مینیمم محلی گفته میشود.
تاثیر نرخ یادگیری در همگرایی گرادیان نزولی
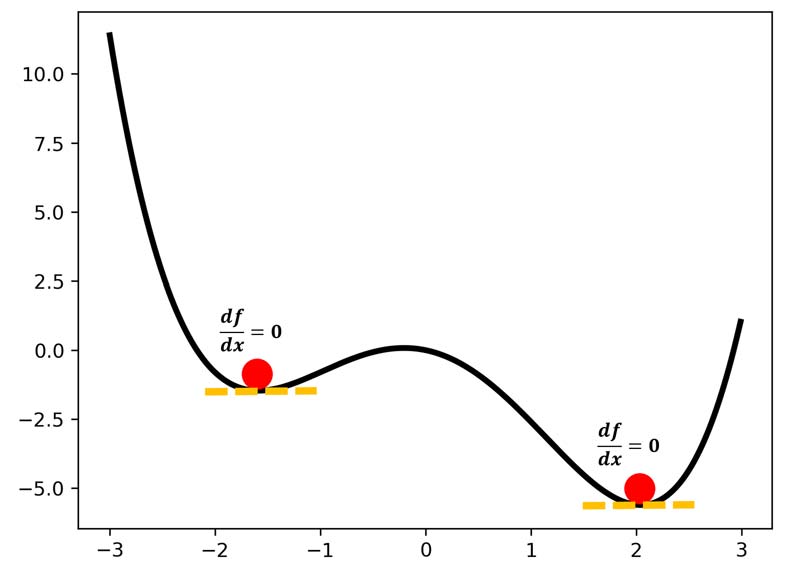
برای همین اگر نرخ یادگیری در گرادیان نزولی را مناسب تعریف نکنیم ممکن است الگوریتم در مینیمم محلی گیر کند و پارامتر بهینه سازی به یک مقدار اشتباه همگرا شود!
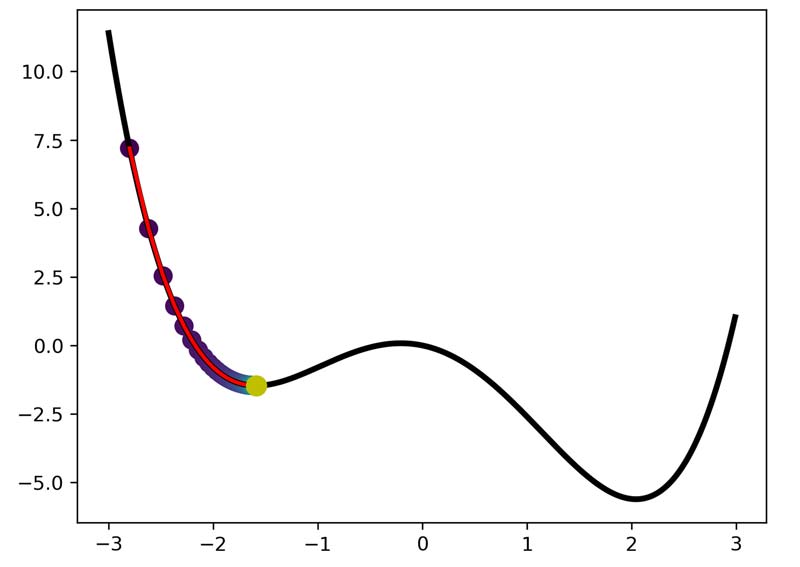
خب راه چاره اینه که نرخ یادگیری را بزرگتر انتخاب کنیم که از الگوریتم از روی این نقاط بپرد! اما مسئله اینه که اگر نرخ یادگیری را هم بزرگ در نظر بگیریم ممکن است از مینیمم اصلی هم بپرد و الگوریتم همانند شکل زیر به حالت ناپایدار برسد!!
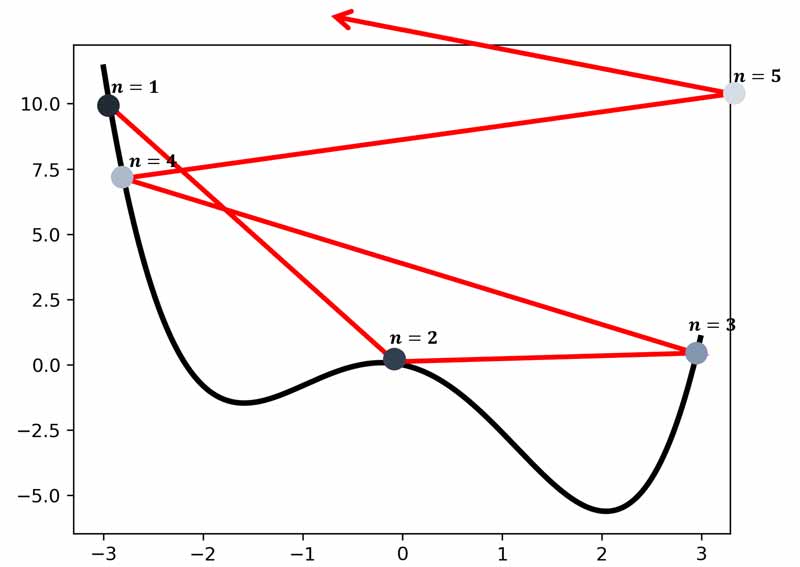
اینجاست که نحوه تعیین نرخ یادگیری در گرادیان نزولی یک کاری بسیار چالشی میشود. تحقیقات زیادی روی این مسئله انجام شده است و راهکارهای مختلفی برای تعیین نرخ یادگیری مناسب ارائه شده است. در پست های آینده این رویکردها را معرفی خواهیم کرد.
در دوره تخصصی پایتورچ این مسائل را به صورت دقیق داریم بررسی میکنیم.
ما در دوره پایتورچ سه هدف اصلی داریم:
- یادگیری تئوری ریاضیات شبکه های عصبی و روشهای بهینه سازی
- یادگیری کار با ابزار پایتورچ به صورت تخصصی
- ساخت dataloader ها اختصاصی برای داده های خودمان
- پیادهسازی شبکه های عصبی با ابزار پایتورچ
- انجام پروژه های عملی

دیدگاه ها