مقدمه‌ای بر EEG Spectrogram (طیف نگاری سیگنال EEG)

پس زمینه‌های نوسانی: سیگنال‌های منظم در برابر سیگنال‌های متغیر

EEG در واقع بازنمایی از پتانسیل‌های پس سیناپسی تولید شده در قشر مغز است. این سیگنال را می‌توان در نقاط زمانی مجزا نمونه برداری کرد (برای این منظور باید از یک فرکانس نمونه برداری مشخص استفاده کرد که مشخص می‌کند در هر ثانیه، چند نمونه از سیگنال استخراج شود). نمونه‌های ولتاژ درون یابی می‌شوند تا در نهایت سیگنالی تولید کنند که بتوان آن را در کامپیوتر نمایش داد. (مانند شکل زیر)

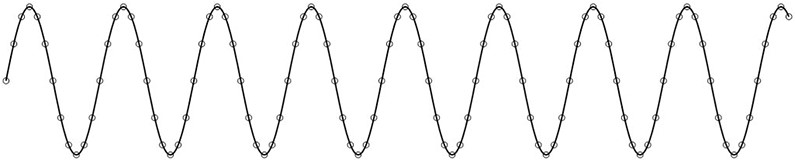
درون یابی نقاط نمونه برداری شده در نقاط زمانی گسسته برای تولید یک سیگنال

در دوره‌های زمانی کوتاه (مثلاً کمتر از 1 ثانیه)، سیگنال‌های EEG اغلب به صورت امواج نوسانی ظاهر می‌شوند. یک سیگنال نوسانی، الگویی منظم با چند ویژگی یا مشخصه‌ی اساسی است که پزشک به دنبال آنهاست (شکل زیر). فرکانس f، تعداد دفعات تکرار موج در طول زمان را نشان می‌دهد. فرکانس بر حسب هرتز (Hz) یعنی تعداد نوسانات در ثانیه اندازه گیری می‌شود. بخش دوم، فاز  θ است که زمانبندی موج نسبت به طول سیکل آن است. تغییر فاز یک سیگنال نوسانی کاملاً منظم به عقب یا جلو در زمان با یک سیکل کامل، موج را به زمانبندی اولیه‌ی خود برمی‌گرداند. فاز بر حسب درجه (°) یا رادیان (واحد  π) اندازه گیری می‌شود. سپس دامنه A است که میانگین فاصله‌ی بین قله‌ها و دره‌های سیگنال است و بر حسب میکروولت(μV) اندازه گیری می‌شود. در نهایت، توان P است که مربع دامنه‌ی A است. توان اغلب در مقیاس لگاریتمی در واحد دسی بل(dB)  نمایش داده می‌شود.

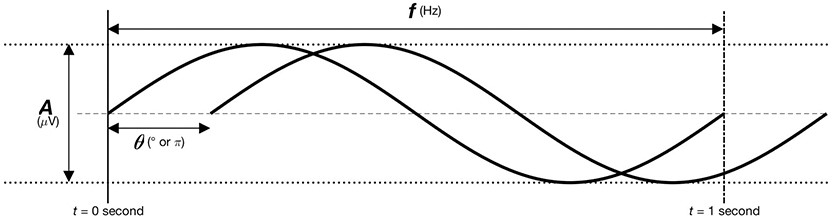
مشخصه‌های موج اولیه

مانند هر سیگنال دیگری، سیگنال EEG نیز یک «طیف» مرتبط دارد به این معنی که همیشه می‌توان سیگنال EEG را به یک سری از امواج سینوسی و امواج کسینوسی تجزیه کرد. همچنین می‌توان سیگنال EEG را از همان طیف امواج سینوسی و کسینوسی بازسازی کرد. طیف امواج سینوسی و کسینوسی را «حوزه‌ی فرکانس» نمایش سیگنال نیز می‌نامند. زیرا خود سیگنال در «حوزه‌ی زمان» است. فرمول ریاضی که به ما امکانی می‌دهد تا تبدیلات بین حوزه‌های زمان و فرکانس سیگنال را انجام دهیم «تبدیل فوریه» نام دارد.

شماتیکی از تبدیل فوریه

برخی از سیگنال‌های نوسانی، طیف‌های بسیار ساده‌ای دارند در حالیکه برخی دیگر، طیف‌های پیچیده‌ای نشان می‌دهند. نوسانات منظم را می‌توان با استفاده از تعداد نسبتاً اندکی از امواج سینوسی وکسینوسی ایجاد کرد. به عنوان مثال یک موج سینوسی خالص فقط شامل یک فرکانس است به این معنی که طیف آن فقط برای همین فرکانس f، دامنه‌ی غیرصفر دارد. در مقابل، سیگنال‌هایی که نامنظم و در حال تغییر هستند، پیچیده‌تر هستند و ترکیبی از نوسانات با طیف وسیع‌تر هستند. متشکل از تعداد بیشتری امواج سینوسی و کسینوسی هستند. این سیگنال‌های EEG را می‌توان به صورت میانگین وزن‌دار خطی از امواج سینوسی و کسینوسی ساخت (یا به آنها تقسیم کرد).

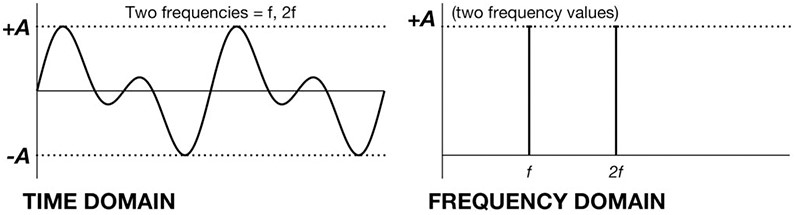
نمونه‌ای از نوسانات ترکیبی در حوزه‌ی زمان و فرکانس

بهترین تقریب برای یک موج سینوسی ساده در EEG واقعی، ریتم غالب  posterior (PDR) در محدوده‌ی فرکانسی آلفا (f= 8-13Hz) است. PDR یک ریتم پس زمینه بیداری طبیعی است که عمدتاً در نواحی پس سری با چشم‌های بسته دیده می‌شود. یک بخش 10 ثانیه‌ای EEG در PDR در شکل زیر نشان داده شده است. طیف توان آن نیز در مقیاس لگاریتمی در واحد dB نشان داده شده است. یک پیک برجسته تقریباً در 9.5 هرتز دیده می‌شود.

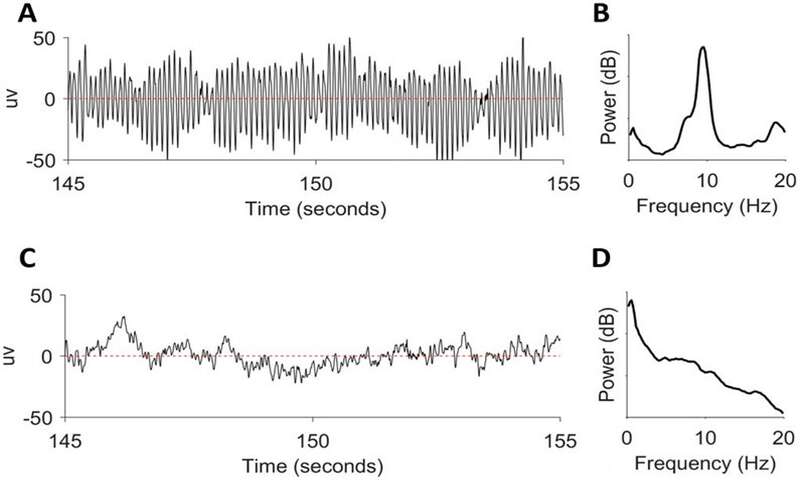
EEG و طیف توان ریتم غالب خلفی (A,B) و سیگنال غیرمنظم (C, D)

برخلاف PDR، بیشتر سیگنال‌های پس زمینه EEG از ترکیب گسترده‌ای از نوسانات تشکیل شده‌اند به جای اینکه از امواج محدود به یک باند باریک فرکانسی تشکیل شده باشند. نمونه‌ای از چنین فرکانس‌های متنوعی در شکل زیر بخش C نشان داده شده است. این سیگنال ترکیبی از نوسانات دلتا، تتا و نوسانات سریعتر است. بر این اساس، طیف در شکل زیر بخش D بالاتر توان را در محدوده‌ی دلتا (0 تا 4 هرتز) نشان می‌دهد. این توان ادامه دارد اما به صورت خطی در محدوده‌ی 0 تا 20 هرتز کاهش می‌یابد.

رویدادهای گذرا (Transient Event)

حتی سیگنال‌های «پیچیده‌تر» از سیگنال‌های نامنظم، رویدادهای گذرای غیرنوسانی با شکلی مشخص هستند مانند یک اسپایک صرعی (epileptic spike). اگرچه EEG پس زمینه ممکن است به عنوان ترکیبی نسبتاً ساده از نوسانات پیوسته در نظر گرفته شود. اما بخش‌های گذرا در سیگنال EEG را می‌توان رویدادهای «پیش زمینه» در نظر گرفت که از پس زمینه جدا می‌شوند و متمایز می‌شوند. مانند سیگنال‌های نوسانی، رویدادهای گذرا را نیز می‌توان به مجموعه‌ای از نوسانات تجزیه کرد. با این حال ساخت چرخش‌های تیز در سیگنال برای ارائه شکل موج تیزتر به نوسانات بیشتری نیاز دارد که به طیف وسیع‌تری تبدیل می‌شود.

ابتدا بیایید یک ترکیب spike-wave با استفاده از نوسانات جزئی بسازیم (شکل زیر). هر چقدر تعداد نوسانات جزئی را بیشتر می‌کنیم، تقریب ما دقیق‌تر می‌شود. در شکل زیر ردیف بالا یک اسپایک و موج (رنگ سیاه) را به همراه تقریب‌های (رنگ قرمز) ساخته شده با استفاده از 2 (سمت چپ ترین ستون) تا 15 (سمت راست‌ترین ستون) مولفه‌ی سینوسی نشان می‌دهد که در ردیف دوم نشان داده شده است و طیف دامنه (دامنه سینوسی هر جز به عنوان تابعی از فرکانس) در ردیف سوم نشان داده شده است.

بخش A) ساخت یک ترکیب spike-wave، بخش B) با اضافه کردن موج‌های سینوسی بیشتر و C) با طیف توانی مربوطه

به طور مشابه، به نوسانات جزئی بیشتری نیاز است تا بخش گذرای باریک‌تری ساخته شود. بنابراین طیف توان یک سیگنال نه تنها تابعی از فرکانس‌های نوسانات پس زمینه است بلکه تابعی از شکل سیگنال است با مشخصه‌های سیگنال تیز یا اسپایکی که اجزای فرکانسی بالاتری را در طیف تولید می‌کنند.

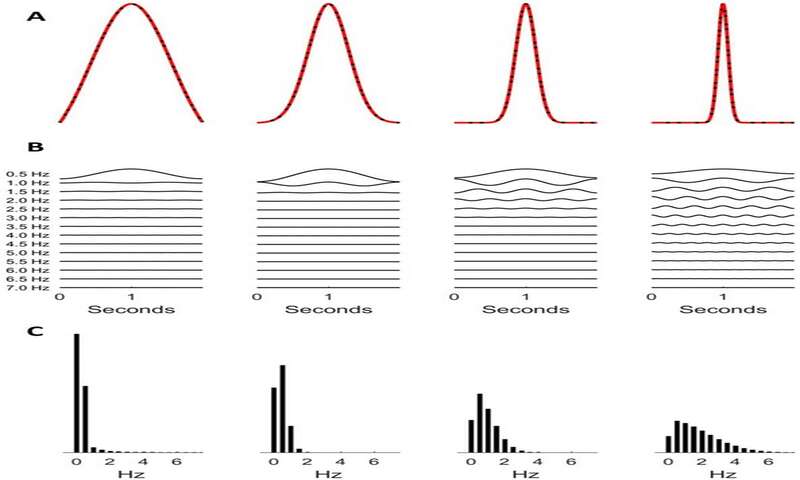
بخش A) ساخت یک موج اسپایکی، بخش B)با اضافه کردن امواج سینوسی بیشتر و C)با طیف توان مربوطه

زمانی که تخلیه‌های صرعی اینترکتال تکراری ایجاد می‌شوند (یعنی به عنوان تخلیه‌های دوره‌ای)، توصیف آنها از نظر نوسانی پیچیده‌تر می‌شود. به جای توصیف رویدادهای جدا شده بر حسب یک طیف و تابعی از دامنه، توصیف طیف به عنوان تابعی از زمان یعنی یک طیف نگار یا spectrogram مفیدتر است.

تحلیل طیفی سیگنال EEG: (Spectral Analysis)

تحلیل طیفی، سیگنال EEG را به تمام فرکانس‌هایی که سیگنال اصلی را ساخته‌اند تجزیه می‌کند و همچنین توان هر فرکانس را نیز محاسبه می‌کند. (توان همان دامنه به توان دو است). این تحلیل یک EEG Spectrum را ایجاد می کند که در شکل زیر می‌بینید.

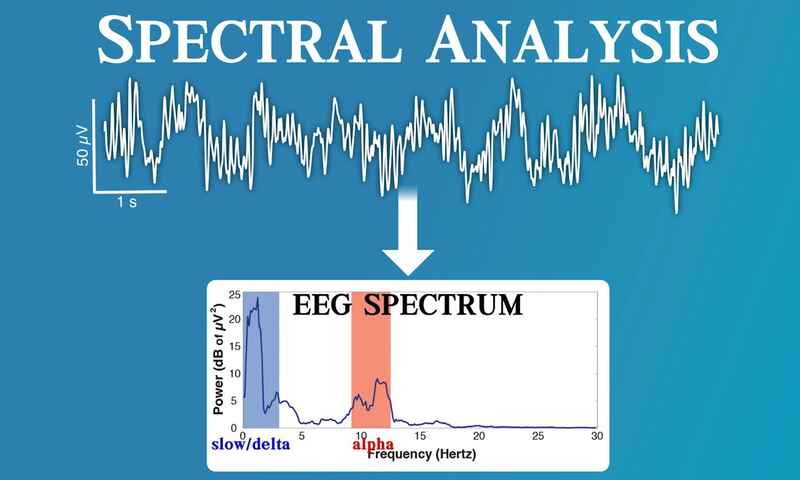
spectrum analysis

این نمودار برای یک سگمنت زمانی از سیگنال EEG است و از آنجاییکه ما می خواهیم الگوی تکاملی EEG را بررسی کنیم، Spectrum را برای هر سگمنت زمانی محاسبه می‌کنیم و شکل زیر بدست می‎‌آید:

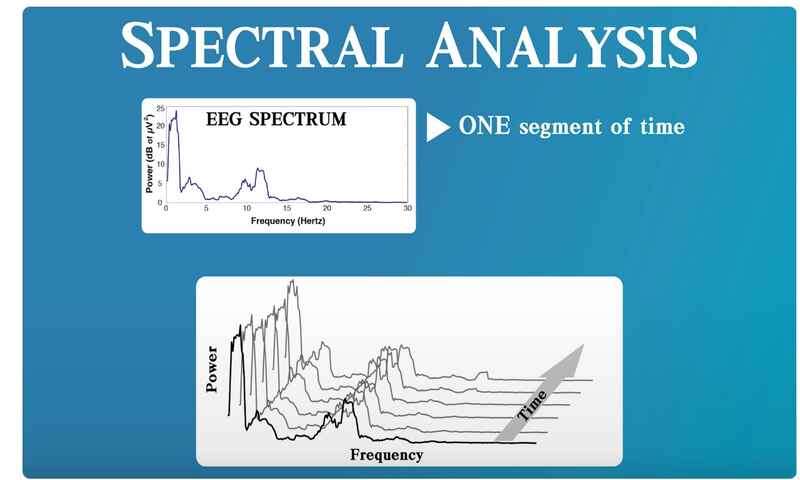
spectral analysis

که در نهایت به شکلی سه بعدی تبدیل می‌شود که ابعاد به ترتیب نشانگر فرکانس، توان و زمان هستند.

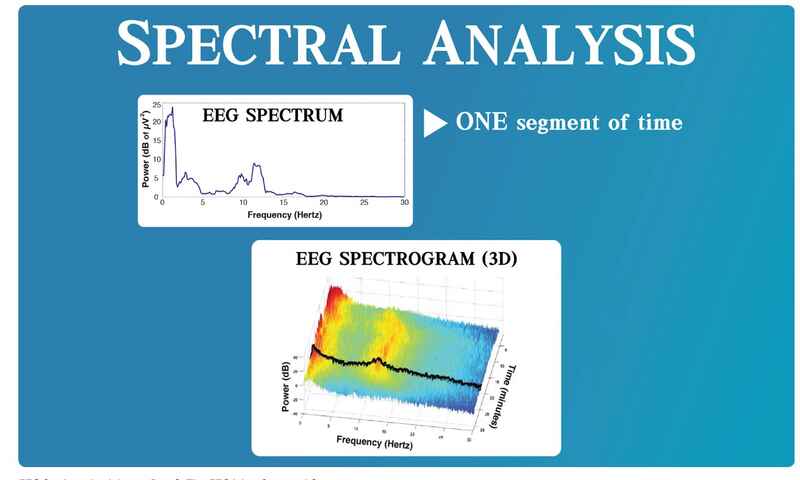
(EEG spectrogram (3D

می‌توان بعد توان (power) را حذف کرد و spectrogram را با دو بعد فرکانس و زمان نمایش داد. با کدگذاری رنگی در نمودار دو بعدی EEG Spectrogram در واقع توان را نشان داده‌ایم.

EEG Spectrogram ها، راهی بهتر برای تحلیل سیگنال‌های EEG فراهم می‌آورند. در شکل زیر به خوبی دو باند فرکانسی را می‌توان تشخیص داد.

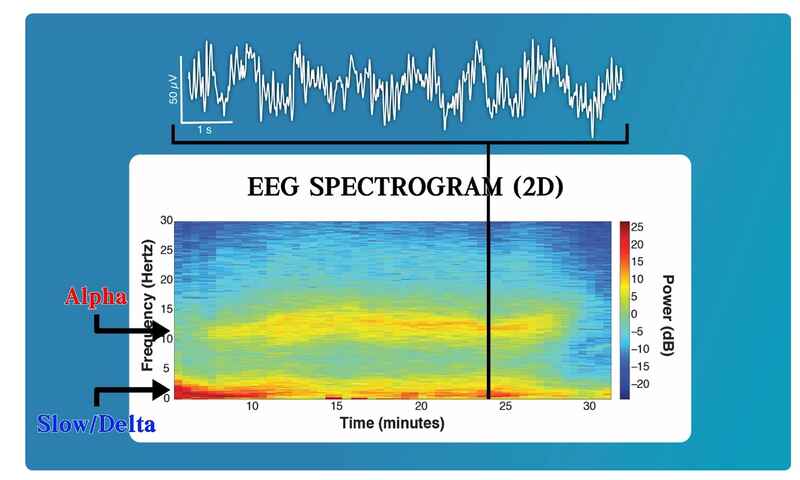
EEG Spectrogram (bands)

پس نیاز است این مراحل طی شوند

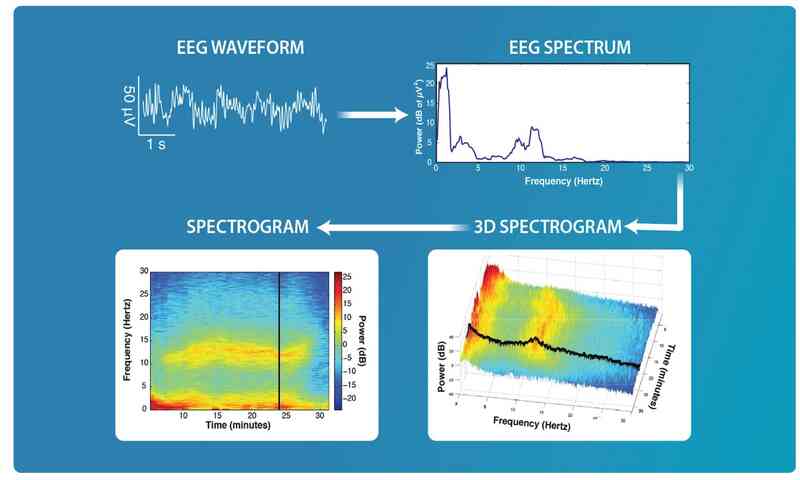
EEG approach

محدودیت‌های Spectrogram: رزولوشن زمانی در برابر رزولوشن طیفی

تا به این جا، تمامی حالات را با این فرض در نظر گرفتیم که اندازه پنجره T ثابت بماند. حالت دیگری در spectrogramها وجود دارد که اندازه پنجره T تغییر می‌کند. به طور خاص، سایز پنجره کوچکتر از زمان T امکانی می‌دهد تا جزئیات زمانی دقیق‌تر (برای مثال وضوح زمانی بهتری) ارائه شود اما به قیمت نویز بیشتر. برای درک بهتر این موضوع به شکل زیر نگاه کنید که بخش A یک سگمنت 20 ثانیه‌ای سیگنال EEG را با تعداد زیادی اسپایک صرعی نشان می‌دهد. در شکل‌های بخش B, C, D، spectrogramهای 20 ثانیه‌ای حاصل به ترتیب با پنجره‌های لغزان T=4,2,1 ثانیه محاسبه می‌شوند. Spectrogram محاسبه شده با بزرگترین پنجره زمانی (T=4s) هموارترین است اما ضعیف‌ترین رزولوشن زمانی را نیز دارد و هیچ یک از اسپایک‌ها به طور مشخص قابل مشاهده نیستند. پنجره‌ی T=1s نویزی‌ترین spectrogram  است.

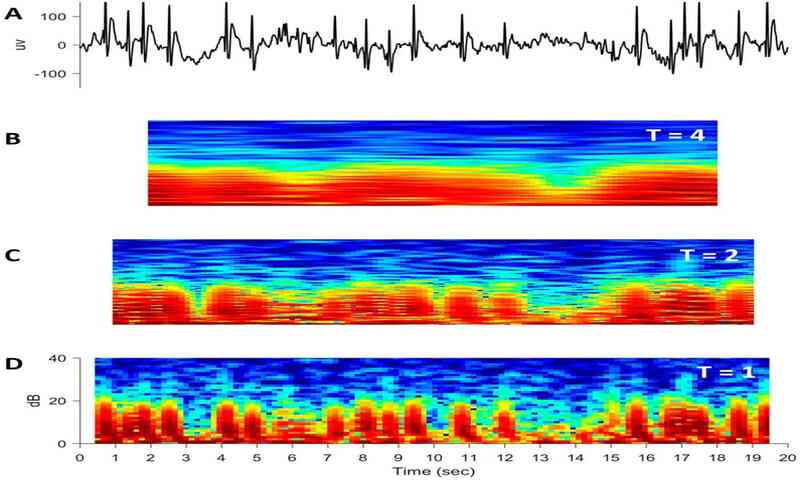
Spectrogramها با سایزهای پنجره مختلف

اگر اندازه پنجره T را برای افزایش رزولوشن زمانی، کاهش دهیم، علاوه بر نویز بیشتر، رزولوشن طیفی را نیز کاهش می‌دهیم. این مسئله از پیامدهای «قضیه نایکوئیست» است که بیان می‌کند حداکثر رزولوشن طیفی( برابر تقریباً دو برابر نرخ نمونه‌برداری) با طول سگمنت سیگنال T رابطه مستقیم دارد. با فرض نرخ نمونه‌گیری ثابت، کوچک شدن اندازه پنجره T، تعداد سینوسی‌های فرکانس بالای موجود برای نمایش سیگنال را کاهش می‌دهد و توانایی ما را برای تشخیص جزئیات دقیق در حوزه فرکانس برای کاهش وضوح طیفی نیز کاهش می‌دهد.

این «ارتباط رزولوشن زمانی-طیفی» از نظر ریاضی مانند اصل عدم قطعیت هایزنبرگ است که ارتباط بین سنجش دقیق موقعیت یا تکانه‌ی یک ذره را توصیف می‌کند. این ارتباط بدین معنی است که رزولوشن طیفی بالاتر به قیمت رزولوشن زمانی ضعیف‌تر است و بالعکس. فرد باید بین نیاز به تفکیک زمانی و طیفی خود تصمیم گیری کند.