تبدیل فوریه زمان کوتاه

ایراد تبدیل فوریه

هدف ما در این پست بررسی ایراد تبدیل فوریه از دید استخراج ویژگی در حوزه فرکانس هست. حال فرض کنید یک مسئله دو کلاسه داریم که در آن هدفمان طراحی سیستمی هست که بتواند دو گروه را با استفاده ویژگیهای حوزه فرکانس سیگنالها تفکیک کند. فرض کنید سیگنال ثبت شده برای گروه اول و دوم به صورت زیر هست.

همانطور که می‌بینیم سیگنالهای دو گروه از لحاظ میزان تغییرات دامنه باهم متفاوت هستند و به عبارتی عکس هم هستند. در گروه اول فرکانس تغییرات دامنه در ابتدا آهسته و سپس رفته رفته بیشتر می شود و در گروه دوم عکس این هست.

حال اگر بخواهیم از سیگنالهای دو گروه در حوزه فرکانس ویژگی استخراج کنیم، لازم است که در ابتدا با کمک تبدیل فوریه سیگنالها را به حوزه فرکانس ببریم و سپس از محتوای فرکانسی آنها ویژگی های مورد نظر را استخراج کنیم. همانطور که در شکل زیر می‌بینید، با اینکه سیگنال ثبت شده برای هر دو گروه کاملا متفاوت بودند، ولی محتوای فرکانسی یکسانی دارند.

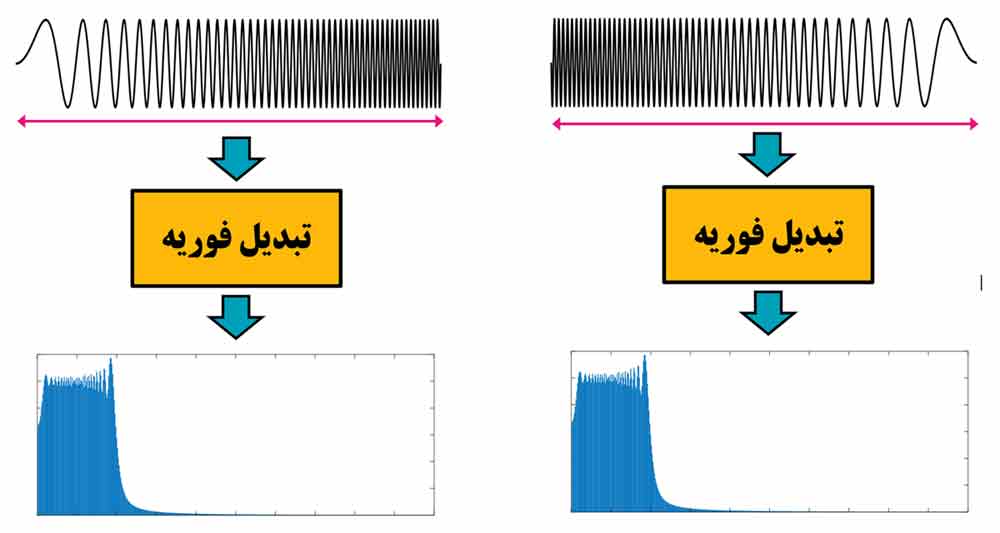
اگر از دو گروه در حوزه فرکانس ویژگی استخراج کنیم، در نتیجه آن داده ها دوگروه در فضای ویژگی کنار هم خواهند بود، و تفکیک پذیر نخواهند بود.

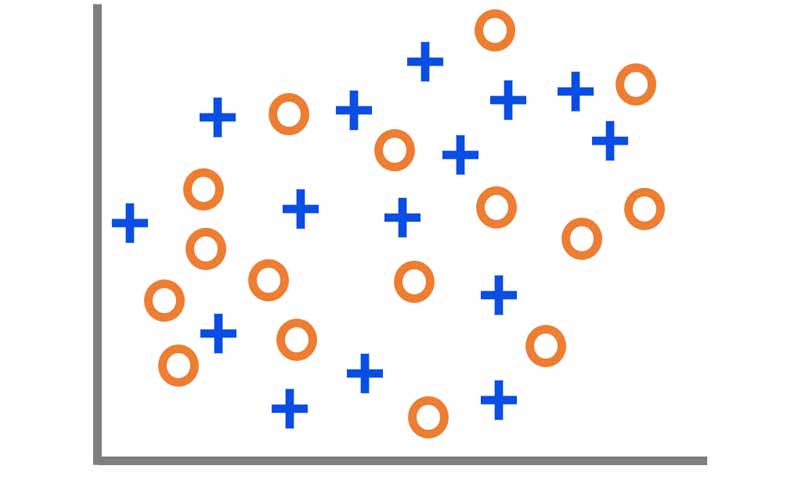
دلیل اینکه دو گروه محتوای فرکانسی یکسانی دارند، به نحوه محاسبه تبدیل فوریه بر میگردد. تبدیل فوریه روی کل بازه زمانی سیگنال اعمال می‌شود. یعنی به اطلاعات زمانی کار ندارد و فقط مشخص می‌کند که سیگنال شامل چه محتوای فرکانسی هست و در چنین مسائلی اطلاعات فرکانسی برای تحلیل دو گروه مناسب نخواهد بود!

صورت مسئله

برای درک بهتر ایراد تبدیل فوریه اجازه بدهید، یک مثال جالب تری بزنیم، تلفنهای خانگی را به خاطر بیارید، همه ما تجربه شماره گیری با این تلفن ها را داشته ایم. ارقام مربوط به شماره فرد مورد نظر را به ترتیب شماره گیری می‌کنیم و بعدش سیستم تلفن متوجه می‌شود که چه شماره ای وارد کرده اید و با فرد مورد نظر تماس را برقرار می‌کند!

حال بیایید ببینیم که سیستم تلفن چطور تشخیص میدهد که چه شماره ای را شما وارد کرده اید. تک تک ارقام یک کد خاصی دارند. این کد مربوط میشه به فرکانس تک موج سینوسی هر شماره. اگه دقت کنید موقع فشار دادن شماره ها یک صدایی(بوق) شنیده می‌شود. هر شماره یک صدای مخصوص به خود دارد. با فشار دادن هر شماره یک موج تک سینوسی با فرکانس مشخصی ایجاد می‌شود که شما صدای بوق می شنوید. این فرکانسها برای سیستم مشخص هست و و با کمک آنها متوجه می شود که چه شماره هایی را فرد شماره گیری کرده است.

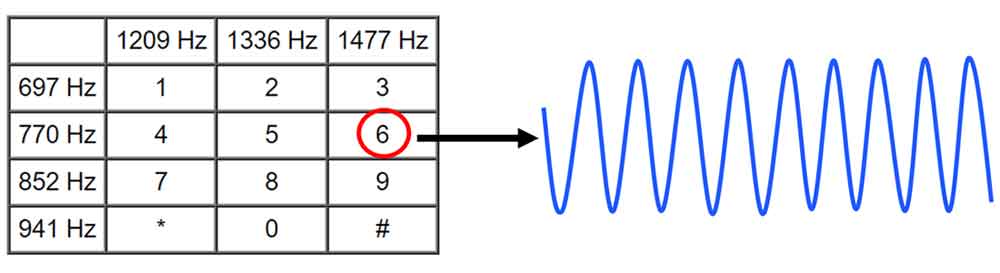
حال بیایید خودمان اینکار را انجام دهیم. فرض کنید یک فردی سه تا شماره 1 و 2 و 3 را شماره گیری کرده است و سیگنال زیر ساخته شده است.

فرض کنید که f2، f1 و f3 به ترتیب فرکانس شماره 1، 2 و 3 باشد و f1<f2<f3 است. و برای شما فرکانس تک تک شماره ها از قبل شناخته شده باشد. حال از شما میخواهند که با تحلیل سیگنال(صوت) ایجاد شده تشخص دهید که کاربر به چه ترتیب سه شماره مورد نظر را شماره گیری کرده است؟

[1,2,3]; [1,3,2]; [2,1,3]; [2,3,1]; [3,2,1]; [3,1,2]

تحلیل سیگنال در حوزه زمان

اگر بخواهیم با تحلیل سیگنال در حوزه فرکانس این مسئله را متوجه بشویم، کار بسیار سخت هست و عملا همچین امکانی وجود ندارد! شما هر بخش سیگنال را زوم بکنید، یک موج سینوسی خواهید دید و از روی اون نمیتوان متوجه شد که مربوط به کدام شماره هست!

تحلیل سیگنال در حوزه فرکانس

اگر بخواهیم با تحلیل سیگنال در حوزه فرکانس این مسئله را بررسی کنیم، لازم است که به کل بازه زمانی سیگنال تبدیل فوریه را اعمال کنیم و به حوزه فرکانس ببریم. شکل زیر نتیجه اعمال تبدیل فوریه به سیگنال را نشان میدهد.

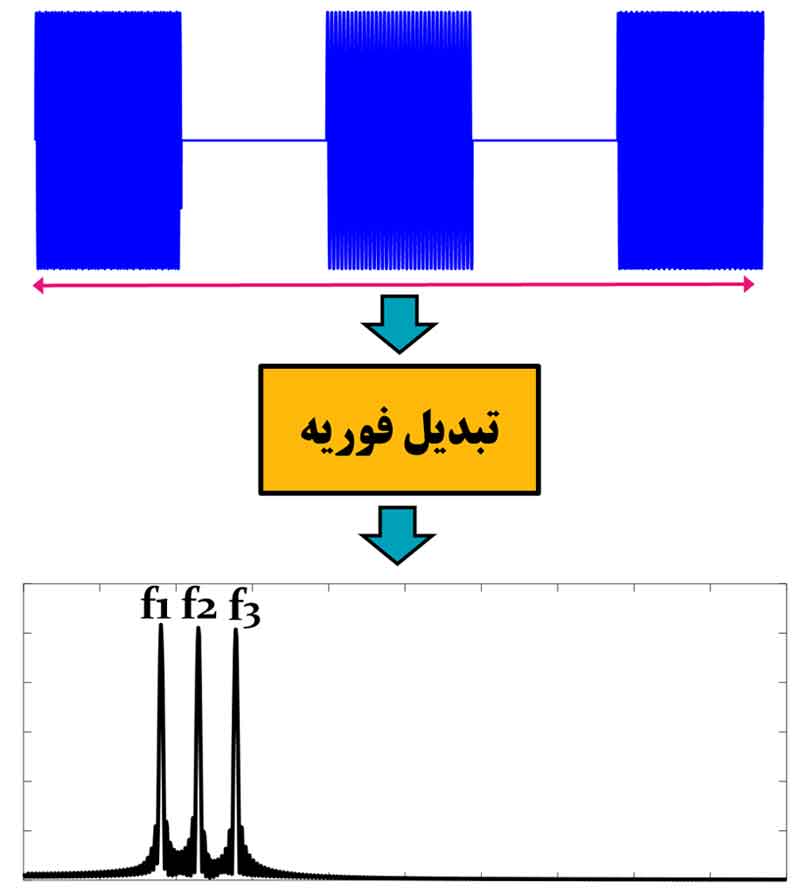
حوزه فرکانس تنها اطلاعاتی که ما به میدهد این است که سیگنال از چه محتوای فرکانسی تشکیل شده است. همانطور که در شکل میبینید، مشخص هست که سیگنال از سه موج تک سینوسی تشکیل شده است. ولی اینکه ترتیب این موجهای سینوسی به چه شکل هست را نمیتوانیم با تحلیل سیگنال در حوزه فرکانس متوجه شویم!

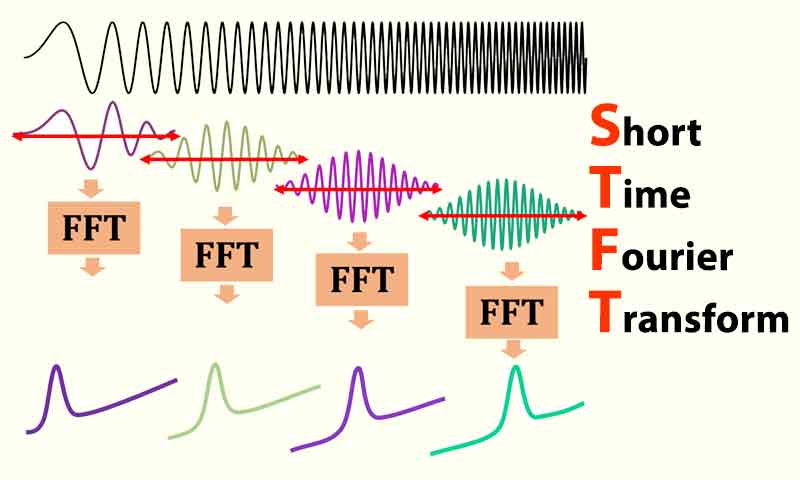
تبدیل فوریه زمان کوتاه(short time fourier transform)

همانطور که دیدیم حوزه زمان و فرکانس هیچ کدام به تنهایی اطلاعات کافی در مورد مسئله مورد نظر ارائه نمیدهند. ولی اگر بتوانیم از اطلاعات هر دو حوزه به طور همزمان استفاده کنیم میتوانیم اطلاعات کافی برای حل مسئله داشته باشیم. برای اینکار لازم است که از تبدیل فوریه زمان کوتاه استفاده کنیم.

در تبدیل فوریه زمان کوتاه، به جای اینکه تبدیل فوریه کل سیگنال یکجا حساب شود، تبدیل فوریه بازه های زمانی کوتاه محاسبه می شود. به این ترتیب که سیگنال را به چندین زیر بخش تقسیم می‌کنیم و سپس روی هر بازه زمانی یک تبدیل فوریه اعمال می‌کنیم. با اینکار به ازای هر بازه ی زمانی کوتاه اطلاعات فرکانسی را جداگانه بدست می آوریم و میتوانیم با داشتن اطلاعات زمانی و فرکانسی به صورت همزمان ترتیب شماره ها را تشخیص دهیم.

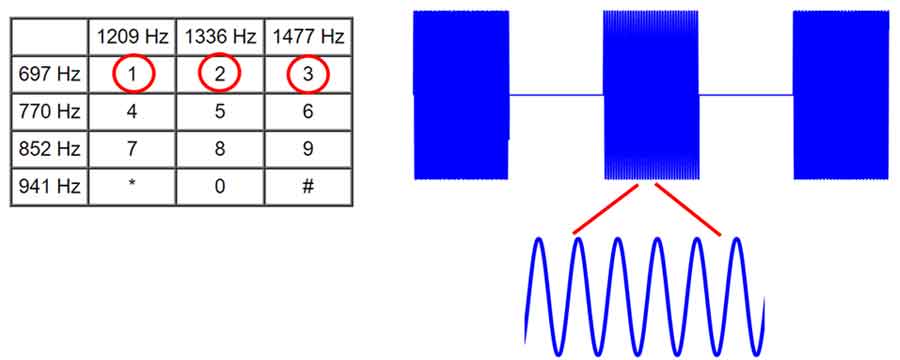
برای مثال اگر بیاییم طبق روال زیر روی هم کدام از موجهای سینوسی سیگنال یک تبدیل فوریه اعمال کنیم، اطلاعات فرکانسی هر کدام را جداگانه خواهیم داشت، و چون از قبل فرکانس هر شماره از قبل برای مشخص هست، با بررسی فرکانس امواج سینوسی در حوزه فرکانس متوجه میشیم که در هر لحظه از زمان چه شماره ای توسط کاربر شماره گیری شده است.

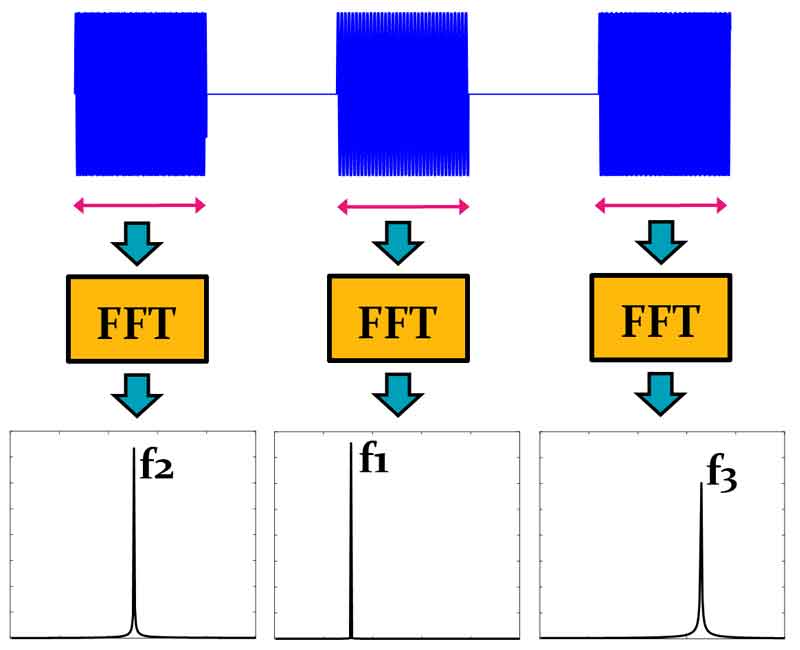
در تبدیل فوریه زمان کوتاه یک پنجره زمانی با طول مشخص توسط کاربر تعیین می شود، سپس سیگنال را به چه چندین بازه ی زمانی کوتاه، به اندازه طول پنجره تقسیم می کنیم، و به ازی هر بازه زمانی یک تبدیل فوریه اعمال میکنیم. و با اینکار به ازای هر بازه ی زمانی، اطلاعات فرکانسی را به صورت جداگانه بدست بیاریم، با این کار اطلاعات زمانی و فرکانسی را به طور همزمان داریم و تحلیل سیگنال برای ما ساده تر میشود.

همانطور که در شکل پیدا هست، فرکانس موج سینوسی بازه زمانی وسطی از همه کمتر هست، و فرکانس موج سینوسی بازه زمانی آخر، از همه بزرگتر و فرکانس موج سینوسی بازه زمانی اول ما بین دو فرکانس هست. بدین معنی است که فرد اول شماره دو و سپس شماره یک و در انتها شماره سه را شماره گیری کرده است. یعنی ترتیب شماره گیری به ترتیب [2,1,3] بوده است.

نوع پنجره تبدیل فوریه زمان کوتاه

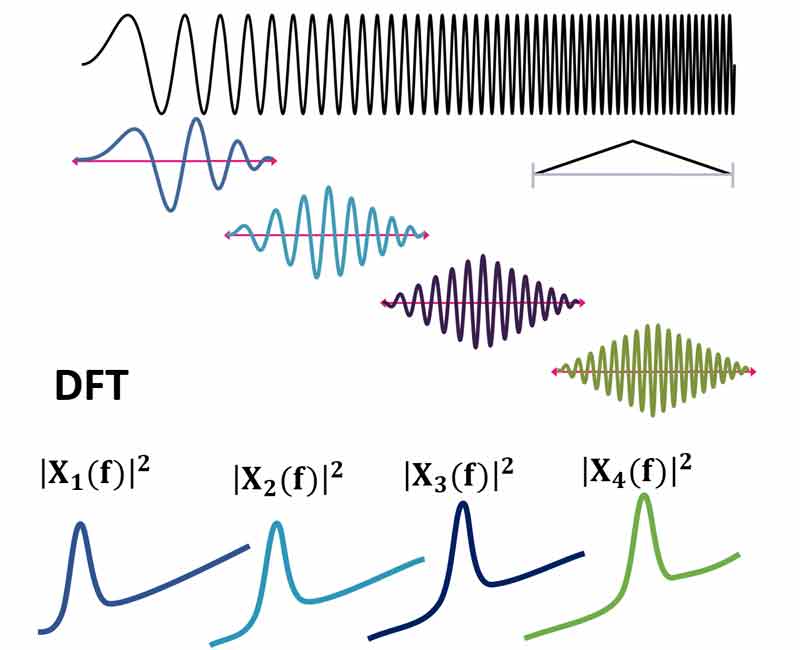
از آنجا که تبدیل فوریه، سیگنال را متناوب در نظر میگیرد، اگر ما تبدیل فوریه سیگنال هر بازه زمانی را مستقیما محاسبه کنیم، اطلاعات فرکانسی سیگنال به خوبی محاسبه نمی‌شود. برای همین قبل از اینکه تبدیل فوریه را روی یک بازه زمانی اعمال کنند، روی سیگنال یک پنجره( از قبیل مثلثیtriangular-، همینگhamming-، هنینگhanning-  و …) اعمال می‌کنند تا از این اثر جلوگیری کند. در شکل زیر نتیجه اعمال پنجره triangular نشان داده شده است.

در دوره پروژه محور “تبدیل فوریه زمان کوتاه در پردازش سیگنال مغزی(EEG)“ مباحث مربوط به تبدیل فوریه زمان کوتاه، اسپکتروگرام و کاربرد آن در پردازش سیگنال مغزی از پایه و به صورت تخصصی همراه با پروژه های عملی آموزش داده ایم. به دوستانی که علاقه مند به این موضوع هستند پیشنهاد میکنیم که این دوره را نگاه کنند. از این مبحث علاوه بر پردازش سیگنال مغزی، در سایر سیگنالهای حیاتی و صوت و غیره میتوانید استفاده کنید.